
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD. 
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=AD=8,求CD的长.
【答案】
(1)证明:∵AD是直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
![]() ,
,
∴Rt△ABD≌Rt△ACD,
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)证明:四边形BFCD是菱形.理由如下:
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中,
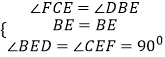 ,
,
∴△BED≌△CEF,
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∴CE2=DEAE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=4,
在Rt△CED中,
CD= ![]() =4
=4 ![]() .
.
【解析】(1)首先证明△ABD≌△ACD,得到∠BAD=∠CAD,再根据等腰三角形的性质即可证明;(2)四边形BFCD的形状是菱形,首先证明△BFE≌△CDE,得到BF=DC,可知四边形BFCD是平行四边形,易证BD=CD,可证明结论;(3)设DE=x,则根据CE2=DEAE列方程求出DE,再用勾股定理求出CD即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是甲、乙、丙三人看地图时对四个地标的描述:
甲:从学校向北直走500公尺,再向东直走100公尺可到图书馆.
乙:从学校向西直走300公尺,再向北直走200公尺可到邮局.
丙:邮局在火车站西方200公尺处.
根据三人的描述,若从图书馆出发,则能走到火车站的走法是( )
A. 向南直走300公尺,再向西直走200公尺
B. 向南直走300公尺,再向西直走600公尺
C. 向南直走700公尺,再向西直走200公尺
D. 向南直走700公尺,再向西直走600公尺
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南有丰富的旅游产品.某校九年级(1)班的同学就部分旅游产品的喜爱情况对游客随机调查,要求游客在列举的旅游产品中选出喜爱的产品,且只能选一项.以下是同学们整理的不完整的统计图: 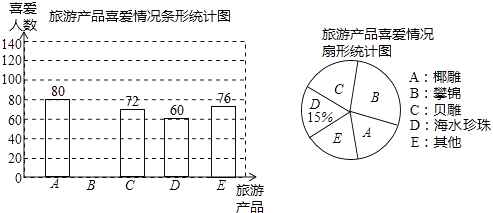
根据以上信息完成下列问题:
(1)请将条形统计图补充完整;
(2)随机调查的游客有人;在扇形统计图中,A部分所占的圆心角是度;
(3)请根据调查结果估计在1500名游客中喜爱攀锦的约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线的研究片断,完成所提出的问题.
探究1:如图(1)在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线,∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB.
∠ACB.
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∴∠BOC=180°-(∠1+∠2)=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A
∠A
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com