
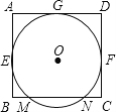
【题目】如图,⊙O与矩形ABCD的边AB,CD,AD相切,切点分别为E,F,G,边BC与⊙O交于M,N两点.下列五组条件中,能求出⊙O半径的有( )①已知AB,MN的长;②已知AB,BM的长;③已知AB,BN的长;④已知BE,BN的长;⑤已知BM,BN的长.
A.2组B.3组C.4组D.5组
【答案】D
【解析】
①连接![]() 、
、![]() 、
、![]() 并反向延长交
并反向延长交![]() 于
于![]() ,根据切线的性质得到
,根据切线的性质得到![]() 过点
过点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求得
,求得![]() ,
,![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,故①正确;
,故①正确;
②根据矩形的性质得到![]() ,∵
,∵![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,故②正确;
,故②正确;
③根据线段的和差得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,故③正确;
,故③正确;
④根据矩形的性质得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() ,故④正确;⑤根据线段的和差和矩形的性质得到
,故④正确;⑤根据线段的和差和矩形的性质得到![]() ,故⑤正确.
,故⑤正确.
①连接![]() 、
、![]() 、
、![]() 并反向延长交
并反向延长交![]() 于
于![]()
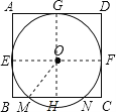
∵![]() 与矩形
与矩形![]() 的边
的边![]() 、
、![]() 、
、![]() 相切,切点分别为
相切,切点分别为![]() 、
、![]() 、
、![]()
∴![]() 过点
过点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中
中
∵![]()
∴![]()
∴已知![]() 、
、![]() 的长,能求出
的长,能求出![]() 半径
半径
∴①正确;
②∵四边形![]() 和四边形
和四边形![]() 是矩形
是矩形
∴![]()
∵![]()
∴![]()
∴在![]() 中
中
∵![]()
∴![]()
∴已知![]() ,
,![]() BM的长,能求出
BM的长,能求出![]() 半径
半径
∴②正确;
③∵![]()
∴![]()
∴在![]() 中
中
∵![]()
∴![]()
∴已知![]() ,
,![]() 的长,能求出
的长,能求出![]() 半径
半径
∴③正确;
④∵四边形![]() 是矩形
是矩形
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴已知![]() ,
,![]() 的长,能求出
的长,能求出![]() 半径
半径
∴④正确;
⑤∵![]()
∴![]()
∴![]()
∵四边形![]() 是矩形
是矩形
∴OE=BH
∴已知![]() ,
,![]() 的长,能求出
的长,能求出![]() 半径
半径
∴⑤正确.
故选:D


科目:初中数学 来源: 题型:
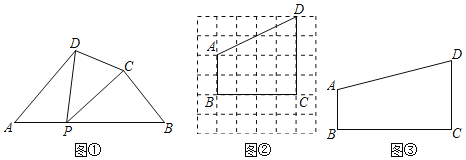
【题目】如图![]() ,在四边形ABCD的边AB上任取一点
,在四边形ABCD的边AB上任取一点![]() 点P不与A,B重合
点P不与A,B重合![]() ,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
,分别连接PD,PC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把P叫四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把P叫做四边形ABCD的边AB上的“强相似点“.
解决问题
![]() 如图
如图![]() ,
,![]() ,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
,试判断点P是否是四边形ABCD的边AB上的相似点,并说明理由.
![]() 如图
如图![]() ,在四边形ABCD中,A,B,C,D四点均在正方形网格
,在四边形ABCD中,A,B,C,D四点均在正方形网格![]() 网格中每个小正方形的边长为
网格中每个小正方形的边长为![]() 的格点
的格点![]() 即每个小正方形的顶点
即每个小正方形的顶点![]() 上,试在图
上,试在图![]() 中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
中画出四边形ABCD的边BC上的相似点,并写出对应的相似三角形;
![]() 如图
如图![]() ,在四边形ABCD中,
,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() 点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
点P在边BC上,若点P是四边形ABCD的边BC上的一个强相似点,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
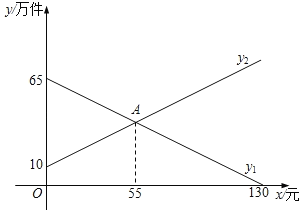
【题目】某商品的市场销售量y1(万件)和生产量y2(万件)都是该商品的定价x(元/件)的一次函数,其函数图象如图所示.
(1)分别求出y1、y2与x之间的函数表达式;
(2)若生产一件该商品成本为10元,未售出的商品一律报废.
①请解释点A的实际意义,并求出此时所获得的利润;
②该商品的定价为多少元时获得的利润最大,最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )
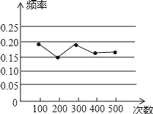
A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某市初中学生上学的交通方式,从中随机调查了a名学生的上学交通方式,统计结果如图.
(1)求a的值;
(2)补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数;
(3)该市共有初中学生15000名,请估计其中坐校车上学的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品的进价为![]() 元,该产品的日销量
元,该产品的日销量![]() (件)是日销价
(件)是日销价![]() (元)的反比例函数,且当售价为每件
(元)的反比例函数,且当售价为每件![]() 元时,每日可售出
元时,每日可售出![]() 件,为获得日利润为
件,为获得日利润为![]() 元,售价应定为________.
元,售价应定为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com