
【题目】探究规律,完成相关题目.
老师说:“我定义了一种新的运算,叫(加乘)运算.”
然后老师写出了一些按照(加乘)运算的运算法则进行运算的算式:
(+5)(+2)=+7;(-3)(-5)=+8;
(-3)(+4)=-7; (+5)(-6)=-11;
0(+8)=8;(-6)0=6.
小明看了这些算式后说:“我知道老师定义的(加乘)运算的运算法则了.”
聪明的你也明白了吗?
(1)归纳(加乘)运算的运算法则:
两数进行(加乘)运算时,运算法则是什么.
特别地,0和任何数进行(加乘)运算,或任何数和0进行(加乘)运算运算法则是什么.
(2)计算:
①(![]() )[
)[![]() (
(![]() )].(括号的作用与它在有理数运算中的作用一致)
)].(括号的作用与它在有理数运算中的作用一致)
② 若(![]() )(
)(![]()
![]() )
)![]() .求
.求![]() 的值.
的值.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l1:y=mx(m≠0) 与直线l2:y=ax+b(a≠0) 相交于点 A(1,2),直线l2与 x轴交于点B(3,0).
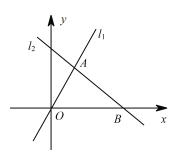
(1)分别求直线l1 和l2的表达式;
(2)过动点P(0,n)且平行于x轴的直线与l1 ,l2的交点分别为C ,D,当点 C 位于点 D 左方时,写出 n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣3经过(﹣1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.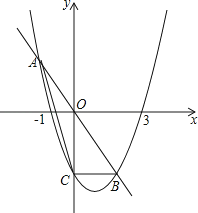
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为 ![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,能否在AB上确定一点E,使△BDE的周长等于AB的长?请说明理由.
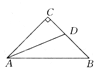
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.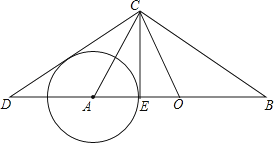
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD= ![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( ) 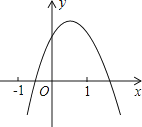
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与坐标轴分别交于A(﹣2,0),B(0,1)两点,与反比例函数的图象在第一象限交于点C(4,n),求一次函数和反比例函数的解析式.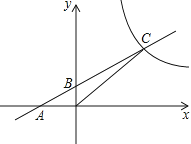
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( ) 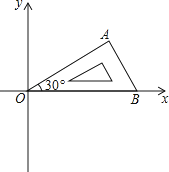
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
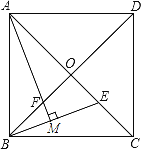
【题目】如图,正方形ABCD的边长为2![]() ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
(1)求证:AF=BE;
(2)求点E到BC边的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com