
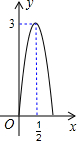
 某市中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为$\frac{1}{2}$米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
某市中心广场有各种音乐喷泉,其中一个喷水管喷水的最大高度为3米,此时距喷水管的水平距离为$\frac{1}{2}$米,在如图所示的坐标系中,这个喷泉的函数关系式是( )| A. | y=-(x-$\frac{1}{2}$)2+3 | B. | y=-3(x+$\frac{1}{2}$)2+3 | C. | y=-12(x-$\frac{1}{2}$)2+3 | D. | y=-12(x+$\frac{1}{2}$)2+3 |
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:选择题
| A. | 5% | B. | 10% | C. | 19% | D. | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.07,$\frac{2}{3}$,$\sqrt{7}$ | B. | 0.7,$\sqrt{5}$,$\sqrt{4}$ | C. | $\sqrt{2}$,$\sqrt{6}$,π | D. | 3.14,$\sqrt{3}$,$\frac{22}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
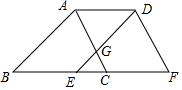 如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为4.
如图,三角形DEF是三角形ABC沿射线BC平移的得到的,BE=2,DE与AC交于点G,且满足DG=2GE.若三角形CEG的面积为1,CE=1,则点G到AD的距离为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
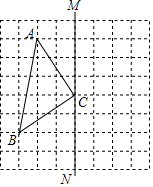 如图,网格中每个小正方形的边长都是1.
如图,网格中每个小正方形的边长都是1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
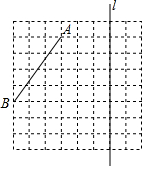 如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.
如图,在8×8的正方形网格纸中每个小正方形的边长都是1,线段AB的端点在小正方形的顶点上,直线l经过网格线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com