
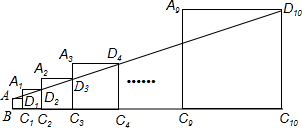
 已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$.
已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$. 分析 延长D4A和C1B交于O,根据正方形的性质和三角形相似的性质即可求得各个正方形的边长,从而得出规律,即可求得正方形A9C9C10D10的边长.
解答  解:延长D4A和C1B交于O,
解:延长D4A和C1B交于O,
∵AB∥A2C2,
∴△AOB∽△D2OC2,
∴$\frac{OB}{O{C}_{2}}$=$\frac{AB}{D{{\;}_{2}C}_{2}}$,
∵AB=BC1=1,D${\;}_{{\;}_{2}}$C2=C1C2=2,
∴$\frac{OB}{O{C}_{2}}$=$\frac{AB}{D{{\;}_{2}C}_{2}}$=$\frac{1}{2}$
∴OC2=2OB,
∴OB=BC2=3,
∴OC2=6,
设正方形A2C2C3D3的边长为x1,
同理证得:△D2OC2∽△D3OC3,
∴$\frac{2}{{x}_{1}}$=$\frac{6}{6+{x}_{1}}$,解得,x1=3,
∴正方形A2C2C3D3的边长为3,
设正方形A3C3C4D4的边长为x2,
同理证得:△D3OC3∽△D4OC4,
∴$\frac{3}{{x}_{2}}$=$\frac{9}{9+{x}_{2}}$,解得x2=$\frac{9}{2}$,
∴正方形A3C3C4D4的边长为$\frac{9}{2}$;
设正方形A4C4C5D5的边长为x3,
同理证得:△D4OC4∽△D5OC5,
∴$\frac{\frac{9}{2}}{{x}_{3}}$=$\frac{\frac{27}{2}}{\frac{27}{2}+{x}_{3}}$,解得x=$\frac{27}{4}$,
∴正方形A4C4C5D5的边长为$\frac{27}{4}$;
以此类推….
正方形An-1Cn-1CnDn的边长为$\frac{{3}^{n-2}}{{2}^{n-3}}$;
∴正方形A9C9C10D10的边长为$\frac{{3}^{8}}{{2}^{7}}$.
故答案为$\frac{{3}^{8}}{{2}^{7}}$.
点评 本题考查了正方形的性质,相似三角形的判定和性质,求得前五个正方形的边长得出规律是解题的关键.


科目:初中数学 来源: 题型:填空题
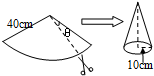 现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为18°.
现有一张圆心角为108°,半径为40cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为18°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
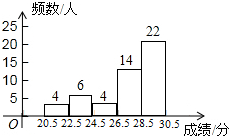 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是92%.
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是92%.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
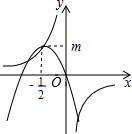 如图,反比例函数y=$\frac{k}{x}$的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,反比例函数y=$\frac{k}{x}$的图象经过二次函数y=ax2+bx图象的顶点(-$\frac{1}{2}$,m)(m>0),则有( )| A. | a=b+2k | B. | a=b-2k | C. | k<b<0 | D. | a<k<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com