
【题目】请完成下列题目:
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°.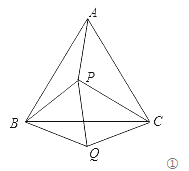
(2)
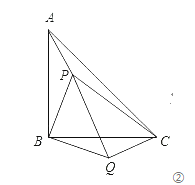
如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明
【答案】
(1)
证明:由旋转的性质知:BP=BQ、PA=QC,∠ABP=∠CBQ;
∵△ABC是等边三角形,
∴∠ABC=60°,即∠CBP+∠ABP=60°;
∵∠ABP=∠CBQ,
∴∠CBP+∠CBQ=60°,即∠PBQ=60°;
又∵BP=BQ,∴△BPQ是等边三角形;
∴BP=PQ;
∵PA2+PB2=PC2,即PQ2+QC2=PC2;
∴△PQC是直角三角形,且∠PQC=90°
(2)
PA2+2PB2=PC2;理由如下:
同(1)可得:△PBQ是等腰直角三角形,则PQ= ![]() PB,即PQ2=2PB2;
PB,即PQ2=2PB2;
由旋转的性质知:PA=QC;
在△PQC中,若∠PQC=90°,则PQ2+QC2=PC2,即PA2+2PB2=PC2;
故当PA2+2PB2=PC2时,∠PQC=90°.
【解析】①由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;
②由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.此题考查了等边三角形、等腰直角三角形的性质,旋转的性质,直角三角形的判定及勾股定理的应用等知识,能够正确的判断出△BPQ的形状,从而得到BP、PQ的数量关系,是解答此题的关键
【考点精析】关于本题考查的等边三角形的性质和勾股定理的逆定理,需要了解等边三角形的三个角都相等并且每个角都是60°;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(2)若在如图三个空格的右侧增加一个空格,将A、B、C、D四个字母任意填写其中(每空填一个字母,每空中的字母不重复),从左往右字母顺序恰好是A、B、C、D的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组 ![]() ,给出下列结论: ①
,给出下列结论: ① ![]() 是方程组的解;
是方程组的解;
②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④x,y的都为自然数的解有4对.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
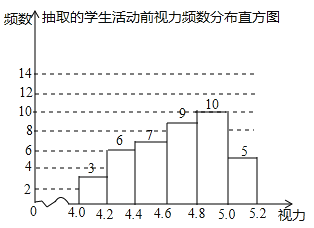
【题目】为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
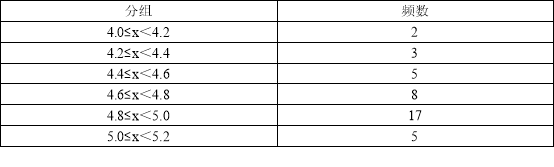
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自由下落物体下落的高度h与下落的时间t之间的关系为h=gt2(g=9.8m/s2),在这个变化中,变量为( )
A. h,t B. h,g C. t,g D. t
查看答案和解析>>
科目:初中数学 来源: 题型:
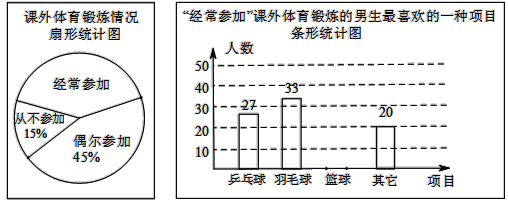
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如图两幅尚不完整的统计图.请根据以上信息解答下列问题:
(1) 课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为____________
(2) 请补全条形统计图
(3) 该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com