
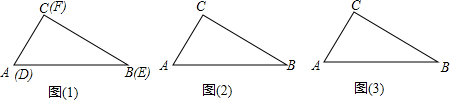
| ||
| 2 |
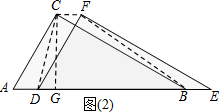 解:(1)如图2,过C点作CG⊥AB于G,
解:(1)如图2,过C点作CG⊥AB于G,| CG |
| AC |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
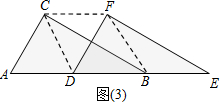 .理由如下:
.理由如下:

科目:初中数学 来源: 题型:
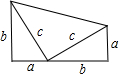 曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为
曾任美国总统的加菲尔德在《新英格兰教育日志》上发表了他提出的一个勾股定理的证明.如图,这就是他用两个全等的直角三角形拼出的图形.上面的图形整体上拼成一个直角梯形.所以它的面积有两种表示方法.既可以表示为查看答案和解析>>
科目:初中数学 来源: 题型:
 25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
25、友情提示:本题有A、B两题,请你任选一题作答,A题满分9分,B题满分12分.若两题都做,只能按A题评分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com