
 已知直线y=$\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B,P是直线AB上的一个动点,过P点分别作x轴、y轴的垂线PE,PF,如图所示,
已知直线y=$\frac{3}{4}$x+3与x轴相交于点A,与y轴相交于点B,P是直线AB上的一个动点,过P点分别作x轴、y轴的垂线PE,PF,如图所示,分析 (1)首先求得点A和点B的坐标,从而得到OB、OA的长度,然后根据勾股定理可求得AB的长,最后根据直角三角形斜边上中线的性质求得OP的长即可;
(2)由正方形的性质可知;点P位于一、三象限或二、四象限的角平分线上,即点P的横纵坐标相等,或互为相反数;
(3)由题意可知四边形OEPF是矩形,由矩形的性质可知OP=EF,然后根据垂线段最短的性质可知OP⊥AB时,EF有最小值,最后利用面积法克求得OP的长,从而得到EF的长.
解答 解;(1)令x=0得:y=3;令y=0得x=-4
∴点A的坐标为(-4,0),点B的坐标为(0,3).
在Rt△ABO中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
在Rt△ABO中,点P是AB的中点,
∴PO=$\frac{1}{2}$AB=$\frac{5}{2}$.
(2)∵四边形PEOF为正方形,
∴PE=PF.
∴点P位于一、三象限或二、四象限的角平分线上.
设点P的坐标为(a,$\frac{3}{4}a+3$),则a+$\frac{3}{4}a+3$=0,或a=$\frac{3}{4}a+3$,
解得a=$-\frac{12}{7}$或a=12
∴点P的坐标为($-\frac{12}{7}$,$\frac{12}{7}$)或(12,12).
(3)如图所示:连接OP.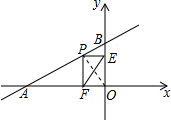
∵∠EOF=∠PEO=∠PFO=90°,
∴四边形PEPF为矩形.
∴PO=EF.
由垂线段最短可知;当OP⊥AB时,OP有最小值.
∵$\frac{1}{2}AB•OP=\frac{1}{2}AO•OB$,
∴$\frac{1}{2}×5×OP=\frac{1}{2}×3×4$.
∴OP=$\frac{12}{5}$.
∴EF存在最小值,最小值为$\frac{12}{5}$.
点评 本题考查的是一次函数的综合应用,解答本题的关键是明确四边形PEOF为正方形时,点P位于一、三象限或二、四象限的角平分线上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)(x+1)=x2-1 | B. | ax-ay+1=a(x-y)+1 | C. | 8a2b2=2a2×4b3 | D. | x2-4=(x+2)(x-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
| 应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
| A. | x与y都是变量,且x是自变量,y是因变量 | |
| B. | 用电量每增加1千瓦时,电费增加0.55元 | |
| C. | 若用电量为8千瓦时,则应交电费4.4元 | |
| D. | 若所交电费为2.75元,则用电量为6千瓦时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 最高气温(℃) | 23 | 24 | 25 | 26 |
| 天数 | 1 | 2 | 1 | 3 |
| A. | 26、25 | B. | 24.5、26 | C. | 26、24.5 | D. | 25、26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com