
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
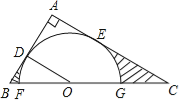
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
【答案】(1)3;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)由AB为圆O的切线,利用切线的性质得到OD垂直于AB,在直角三角形BDO中,利用锐角三角函数定义,根据tan∠BOD及BD的值,求出OD的值即可;
(2)连接OE,由AE=OD=3,且OD与AE平行,利用一组对边平行且相等的四边形为平行四边形,根据平行四边形的对边平行得到OE与AD平行,再由DA与AE垂直得到OE与AC垂直,即可得证;
(3)阴影部分的面积由三角形BOD的面积+三角形ECO的面积﹣扇形DOF的面积﹣扇形EOG的面积,求出即可.
解:(1)∵AB与圆O相切,
∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD=![]() =,
=,
∴OD=3;
(2)连接OE,
∵AE=OD=3,AE∥OD,
∴四边形AEOD为平行四边形,
∴AD∥EO,
∵DA⊥AE,
∴OE⊥AC,
又∵OE为圆的半径,
∴AE为圆O的切线;
(3)∵OD∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AC=7.5,
∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=×2×3+×3×4.5﹣![]()
=3+![]() ﹣
﹣![]()
=![]() .
.



科目:初中数学 来源: 题型:
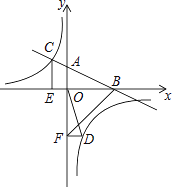
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F连接OD、BF,如果![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
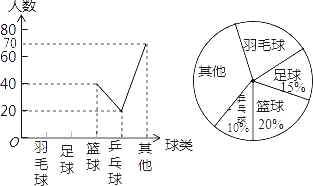
【题目】某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
(1)求出被调查的学生人数;
(2)把折线统计图补充完整;
(3)小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
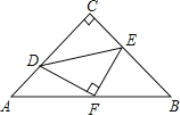
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE;②四边形CDFE不可能是正方形;③△DFE是等腰直角三角形;④S四边形CDFE=![]() S△ABC.上述结论中始终正确的有______.(填序号)
S△ABC.上述结论中始终正确的有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面为某年11月的日历:
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)在日历上任意圈出一个竖列上相邻的3个数;
①设中间的一个数为![]() ,则另外的两个数为 、 ;
,则另外的两个数为 、 ;
②若已知这三个数的和为42,则这三天都在星期 ;
(2)在日历上用一个小正方形任意圈出其中的9个数,设圈出的9个数的中心的数为b,若这9个数的和为153,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州地铁1号线,西起杏山子大道,止于高铁徐州东站,共设18座站点,18座站点如下所示.徐州轨道交通试运营期间,小苏从苏堤路站开始乘坐地铁,在地铁各站点做志愿者服务,到![]() 站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):
站下车时,本次志愿者服务活动结束,约定向徐州东站站方向(即箭头方向)为正,当天的乘车记录如下(单位:站):![]() ,-2,-6,
,-2,-6,![]() 8,
8,![]() 3,-4,-9,
3,-4,-9,![]() 8.
8.


(1)请通过计算说明![]() 站是哪一站?
站是哪一站?
(2)如果相邻两站之间的距离为![]() 千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
千米,求这次小苏志愿服务期间乘坐地铁行进的总路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b, A、B两点之间的距离表示为AB,若a≥b,则 | a-b | = a-b;若a < b,则 | a-b | = b-a,当A、B两点中有一点在原点时, 不妨设点A在原,
如图甲, AB = OB =∣b∣=∣a b∣;当A、B两点都不在原点时,
![]()
① 如图乙,点A、B都在原点的右边,AB=OBOA=|b||a|=ba =|ab |;
![]()
②如图丙,点A、B都在原点的左边, AB = OB OA =|b||a|= b (a) = |ab|;
![]()
③如图丁,点A、B在原点的两边AB=OA+OB=|a|+|b|=a+(b) =|ab|.
![]()
综上所述,数轴上A、B两点之间的距离AB=∣ab∣.
(2)回答下列问题:
①数轴上表示1和3的两点之间的距离是______,数轴上表示1和3的两点之间的距离是______;
②数轴上表示x和1的两点分别是点A和B,则A、B之间的距离表示为______,如果AB=2,那么x =________ ;
③当代数式∣x +1∣+∣x 3∣取最小值时,相应的x的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一边长为![]() 厘米的正方形纸板的四个角各剪去一个边长为
厘米的正方形纸板的四个角各剪去一个边长为![]() 厘米的小正方形,然后把它折成一个无盖纸盒.
厘米的小正方形,然后把它折成一个无盖纸盒.
(1)该纸盒的高是 厘米,底面积是 平方厘米;
(2)该纸盒的全面积(外表面积)为 平方厘米;
(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时![]() 与
与![]() 之间的倍数关系.(直接写出答案即可)
之间的倍数关系.(直接写出答案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com