
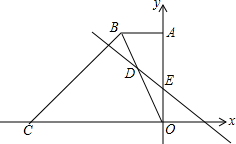
 Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬Ö±½Ç̀ƯĐÎOABCµÄ±ßOC£¬OA·Ö±đÓëxÖᣬyÖáÖغϣ¬AB¡ÎOC£¬¡ÏAOC=90¡ă£¬¡ÏBCO=45¡ă£¬BC=6$\sqrt{2}$£¬µăCµÄ×ø±êΪ£¨-9£¬0£©£®
Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬Ö±½Ç̀ƯĐÎOABCµÄ±ßOC£¬OA·Ö±đÓëxÖᣬyÖáÖغϣ¬AB¡ÎOC£¬¡ÏAOC=90¡ă£¬¡ÏBCO=45¡ă£¬BC=6$\sqrt{2}$£¬µăCµÄ×ø±êΪ£¨-9£¬0£©£®·ÖÎö £¨1£©ÓÉ̉»Ôª¶₫´Î·½³̀µÄ½â£¬È·¶¨³ö0E£¬OC£¬ÔÙ¸ù¾Ư¹´¹É¶¨ÀíµĂ³öBG£¬CG£¬´Ó¶øµĂ³ö½áÂÛ£»
£¨2£©ÓÉDH¡ÎAB£¬µĂ³ö $\frac{OD}{OB}$=$\frac{DH}{AB}$=$\frac{OH}{OA}$£¬Çó³öµăDµÄ×ø±ê£¬ÓÉD£¬EÈ·¶¨³öÖ±ÏßDE½âÎöʽ£»
£¨3£©ÏÈÈ·¶¨³öOE£¬OF£¬ÔÙ·ÖËÄÖÖÇé¿ö¼ÆËă£¬ÓÉÁâĐεÄĐÔÖʺͶԳƼ´¿É£®
½â´đ £¨1£©Èçͼ1£¬
¡ßx2-11x+18=0£¬
¡àx=2»̣x=9£¬
¡ßOE£¼OC£¬
¡àOE=2£¬OC=9£¬
¹ưµăB×÷BG¡ÍOC£¬´¹×ăΪG
¡ß¡ÏOCB=45¡ă£¬BC=6 $\sqrt{2}$£¬
¡àBG=CG=6£¬
¡àOG=3£¬
¡àB£¨-3£¬6£©£¬
£¨2£©Èçͼ2£¬
¹ưµăD×÷DH¡ÎAB£¬½»yÖáÓÚµăH
¡à$\frac{OD}{OB}$=$\frac{DH}{AB}$=$\frac{OH}{OA}$£¬
¡ßOD=2BD£¬
¡àDH=2£¬OH=4£¬
¡àD£¨-2£¬4£©£¬
ÉèÖ±ÏßDE½âÎöʽΪy=kx+b£¬
¹ưµăD£¨-2£¬4£©£¬E£¨0£¬2£©£¬
¡àDE½âÎöʽΪ y=-x+2£»
£¨3£©´æÔÚQ£¬
ÉèÖ±Ïßy=-x+2·Ö±đÓëxÖá¡¢yÖá½»ÓÚµăE¡¢µăF£¬
ỘE£¨0£¬2£©£¬F£¨2£¬0£©£¬
OE=OF=2£¬EF=2 $\sqrt{2}$£®
Èçͼ3Ëùʾ£¬
ÓĐËĸöÁâĐÎÂú×ằẩ⣮
¢ÙÁâĐÎOEP1Q1£¬´ËʱOEΪÁâĐÎ̉»±ß£®
ỘÓĐP1E=P1Q1=OE=2£¬P1F=EF-P1E=2 $\sqrt{2}$-2£®
¡ß¡÷P1NFΪµÈÑüÖ±½ÇÈư½ÇĐΣ¬
¡àP1N=NF=$\frac{\sqrt{2}}{2}$P1F=2-$\sqrt{2}$£»
ÉèP1Q1½»xÖáÓÚµăN£¬
¡àNQ1=P1Q1-P1N=2-£¨2-$\sqrt{2}$£©=$\sqrt{2}$£¬
¡ßON=OF-NF=$\sqrt{2}$£¬
¡àQ1£¨ $\sqrt{2}$£¬-$\sqrt{2}$£©£»
¢ÚÁâĐÎOEP2Q2£¬´ËʱOEΪÁâĐÎ̉»±ß£®
´ËʱQ2ÓëQ1¹ØÓÚÔµă¶Ô³Æ£¬
¡àQ2£¨-$\sqrt{2}$£¬$\sqrt{2}$£©£»
¢ÛÁâĐÎOEQ3P3£¬´ËʱOEΪÁâĐÎ̉»±ß£®
´ËʱP3ÓëµăFÖغϣ¬ÁâĐÎOEQ3P3ΪƠư·½ĐΣ¬
¡àQ3£¨2£¬2£©£»
¢ÜÁâĐÎOP4EQ4£¬´ËʱOEΪÁâĐζԽÇÏߣ®
ÓÉÁâĐÎĐÔÖÊ¿ÉÖª£¬P4Q4ΪOEµÄ´¹Ö±Æ½·ÖÏߣ¬
ÓÉOE=2£¬µĂP4×Ư×ø±êΪ1£¬
´úÈëÖ±Ïß½âÎöʽy=-x+2£¬µĂP4ºá×ø±êΪ1£¬
ỘP4£¨1£¬1£©£¬
ÓÉÁâĐÎĐÔÖÊ¿ÉÖª£¬P4¡¢Q4¹ØÓÚOE»̣xÖá¶Ô³Æ£¬
¡àQ4£¨-1£¬1£©£®
×ÛÉÏËùÊö£¬´æÔÚµăQ£¬Ê¹̉ÔO¡¢E¡¢P¡¢QΪ¶¥µăµÄËıßĐÎÊÇÁâĐΣ»
µăQµÄ×ø±êΪ£ºQ1£¨ $\sqrt{2}$£¬-$\sqrt{2}$£©£¬
Q2£¨-$\sqrt{2}$£¬$\sqrt{2}$£©£¬
Q3£¨2£¬2£©£¬Q4£¨-1£¬1£©£®
µăÆÀ ±¾̀⿼²éÊÇËıßĐÎ×ÛºÏ̀⣬Óõ½µÄ֪ʶµăÊÇ̉»´Îº¯ÊưµÄͼÏóÓëĐÔÖÊ¡¢ÏàËÆÈư½ÇĐεÄÅж¨ÓëĐÔÖÊ£¬¶Ô³ÆµÄĐÔÖÊ£¬¹Ø¼üÊǸù¾ƯÏàËÆÇó³öÏ߶εij¤¶ÈµĂ³öµăµÄ×ø±ê£¬Ñ§»á·ÖÀà̀ÖÂÛ£¬²»ÄÜ©½â£¬ÊôÓÚÖĐ¿¼Ñ¹Öá̀⣮



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â

²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | Ö»ÓĐ·ûºÅ²»Í¬µÄÁ½¸öÊư»¥ÎªÏà·´Êư | B£® | ÓĐÀíÊư·ÖΪƠưÓĐÀíÊưºÍ¸ºÓĐÀíÊư | ||
| C£® | Á½ÊưÏà¼Ó£¬ºÍ̉»¶¨´óÓÚÈκÎ̉»Êư | D£® | ÁăÊÇ×ÔÈ»Êư£¬µ«²»ÊÇÓĐÀíÊư |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
 ̉ÑÖª£ºÈçͼ£¬DE¡ÎBC£¬EF¡ÎCD£¬ÇóÖ¤£ºAD2=AF•AB£®
̉ÑÖª£ºÈçͼ£¬DE¡ÎBC£¬EF¡ÎCD£¬ÇóÖ¤£ºAD2=AF•AB£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
 Èçͼ£¬̉»¼Ü³¤25mµÄÔÆ̀Ưб¿¿ÔÚ̉»ĂæǽÉÏ£¬´Ëʱ̀Ư×ӵ׶ËÀëǽ7m£¬Èô½«̀Ư×ӵĶ¥¶ËÏ»¬4m£¬Ộ̀Ư×ӵĵ׶ËÔÚˮƽ·½Ị̈ÉÏ»¬¶¯ÁË8m£®
Èçͼ£¬̉»¼Ü³¤25mµÄÔÆ̀Ưб¿¿ÔÚ̉»ĂæǽÉÏ£¬´Ëʱ̀Ư×ӵ׶ËÀëǽ7m£¬Èô½«̀Ư×ӵĶ¥¶ËÏ»¬4m£¬Ộ̀Ư×ӵĵ׶ËÔÚˮƽ·½Ị̈ÉÏ»¬¶¯ÁË8m£®²é¿´´đ°¸ºÍ½âÎö>>
°Ù¶ÈÖÂĐÅ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com