

分析 (1)根据正方形的性质得到AE=AG,AB=AD,∠EAB=∠GAD,根据“SAS”可判断△ABE≌△ADG,则△ABE的面积=△ADG的面积;
(2)作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,根据等角的余角相等得到∠PAE=∠GAH,根据“AAS”可判断△AHG≌△AEP,所以GH=BP,然后根据三角形面积公式得到△ABE的面积=△ADG的面积;
(3)由(2)容易得出结论;’
(4)先根据三角形面积公式得到△ABC的面积=$\frac{1}{2}$×4×5×sin∠BAC,利用正弦的定义得到△ABC面积的最大值;然后根据(2)中的结结论计算阴影部分的面积和的最大值.
解答 解:(1)∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上
∴AE=AG,AB=AD,∠EAB=∠GAD=90°,
在△ABE和△ADG中$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠EAB=∠GAD}&{\;}\\{AE=AG}&{\;}\end{array}\right.$
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
故答案为:△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下: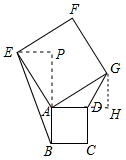
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图所示,
∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中,$\left\{\begin{array}{l}{∠GAH=∠EAP}&{\;}\\{∠GHA=∠EPA}&{\;}\\{AG=AE}&{\;}\end{array}\right.$,
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABE的面积=$\frac{1}{2}$EP•AB,△ADG的面积=$\frac{1}{2}$GH•AD,
∴△ABE的面积=△ADG的面积;
故答案为:△ABE的面积=△ADG的面积;
(3)由(2)得:S△ABC=S△AEN=S△BMF=S△DCG,
故答案为:S△ABC=S△AEN=S△BMF=S△DCG,
(4)∵AB=5m,AC=4m,
∴△ABC的面积=$\frac{1}{2}$×5×4×sin∠BAC=10sin∠BAC,
当sin∠BAC=1时,△ABC的面积的最大值为10,
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=3×10=30m2.
故答案为:30m2.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、三角形的面积计算等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
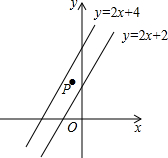 如图,在平面直角坐标系中,点P(-$\frac{1}{2}$,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是1<a<3.
如图,在平面直角坐标系中,点P(-$\frac{1}{2}$,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是1<a<3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
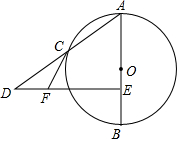 如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F.
如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.767×1013 | B. | 6.767×1012 | C. | 67.67×1012 | D. | 6.767×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 睡眠时间x(小时) |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
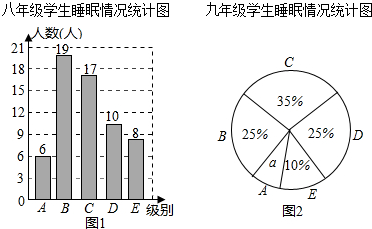
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
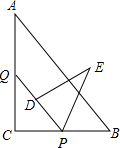 如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com