
| ���۷�ʽ | �ּӹ������� | ���ӹ������� |
| ÿ�ֻ�����Ԫ�� | 1000 | 2000 |
���� ��1�����������ϵΪ�����ӹ�����+�ּӹ�����=15�������г�������⼴�ɣ�
��2������������ӹ���������ȡֵ��Χ��Ȼ���ʾW�����W���ֵ��
��� �⣺��1����ÿ�쾫�ӹ�x�֣���ÿ��ּӹ�3x�֣�������ã�
$\frac{20}{x}$+$\frac{140-20}{3x}$=15��
��ã�x=4��
������ã�x=4��ԭ���̵ĸ���
��3x=12��
��ÿ�쾫�ӹ�4�֣���ÿ��ּӹ�12�֣�
��2���辫�ӹ���ʱ��Ϊm�죬�������m+$\frac{140-4m}{12}$��13��
��ã�m��2��
��ӹ������߲˿ɻ���WԪ����
W=2000•4m+1000•��140-4m��=140000+4000m��Ԫ����0��m��2����
��һ�κ�������֪��W��m�����������
�ʵ�m=2ʱ��Wȡ�����ֵΪ140000+4000��2=148000��Ԫ����
�𣺰���2����о��ӹ���11��ּӹ��ɻ��������Ϊ148000Ԫ��
���� ���⿼���˷�ʽ���̵�Ӧ���Լ�һԪһ�β���ʽ��Ӧ�ú�һ�κ�����Ӧ�ã�����ؼ����ڿ������⣬�ҵ���ȷ�ĵ�����ϵ���г�����ʽ��������𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������������ͼ��ʾ�Ĺ���������ȥ����������ʵ���ԣ�n��m����ʾ��n�ţ������ҵ�m�������磨4��3����ʾʵ��9����11��5����ʾ��ʵ����60��
������������ͼ��ʾ�Ĺ���������ȥ����������ʵ���ԣ�n��m����ʾ��n�ţ������ҵ�m�������磨4��3����ʾʵ��9����11��5����ʾ��ʵ����60���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ƽ���ı��� | C�� | ������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
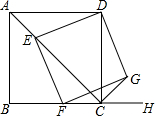 ��ͼ����֪�ı���ABCDΪ�����Σ�AB=$2\sqrt{2}$����EΪ�Խ���AC��һ���㣬����DE������E��EF��DE��������BC�ڵ�F����DE��EFΪ�ڱ�������DEFG������CG��
��ͼ����֪�ı���ABCDΪ�����Σ�AB=$2\sqrt{2}$����EΪ�Խ���AC��һ���㣬����DE������E��EF��DE��������BC�ڵ�F����DE��EFΪ�ڱ�������DEFG������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
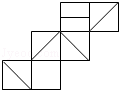 ��ͼ��������ֽ�е�����棬�����������۵����ɵ��ǣ�������
��ͼ��������ֽ�е�����棬�����������۵����ɵ��ǣ�������| A�� | 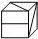 | B�� | 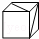 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com