
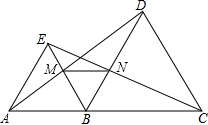
 如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:①②③
如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:①②③分析 可先证明△ABD≌△EBC,可判断①;再证明△ABM≌△EBM,可判断②;可证明△BMN为等边三角形,可判断③;利用等边三角形的三线合一可判断④,可求得答案.
解答 解:
∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中
$\left\{\begin{array}{l}{AB=BE}\\{∠ABD=∠EBC}\\{BD=BC}\end{array}\right.$
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中
$\left\{\begin{array}{l}{∠MAB=∠NEB}\\{AB=BE}\\{∠ABE=∠EBN}\end{array}\right.$
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
综上可知正确的有①②③,
故答案为:①②③.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和性质(即全等三角形的对应边相等、对应角相等).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
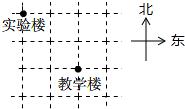 某学校的平面示意图如图所示,请用两种不同的方法表示出实验楼相对于教学楼的位置.图中小方格边长代表实地距离50(单位:m),对角线长代表实地距离70.7(单位:m).
某学校的平面示意图如图所示,请用两种不同的方法表示出实验楼相对于教学楼的位置.图中小方格边长代表实地距离50(单位:m),对角线长代表实地距离70.7(单位:m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2 |
| 筐数 | 1 | 4 | 2 | 4 | 1 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )
如图,△ABC和△DCE都是直角三角形,其中一个三角形是由另一个三角形旋转得到的,下列叙述中错误的是( )| A. | 旋转中心是点C | |
| B. | 顺时针旋转角是90° | |
| C. | 旋转中心是点B,旋转角是∠ABC | |
| D. | 既可以是逆时针旋转又可以是顺时针旋转 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com