
 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.分析 (1)根据中位线的性质得到DP∥AB,DP=$\frac{1}{2}$AB,由SAS可证△CDP≌△POB;
(2)①当四边形AOPD的AO边上的高等于半径时有最大面积,依此即可求解;
②根据有一组对应边平行且相等的四边形是平行四边形,可得四边形BPDO是平行四边形,再根据邻边相等的平行四边形是菱形,以及等边三角形的判定和性质即可求解.
解答 (1)证明:∵PC=PB,D是AC的中点,
∴DP∥AB,
∴DP=$\frac{1}{2}$AB,∠CPD=∠PBO,
∵BO=$\frac{1}{2}$AB,
∴DP=BO,
在△CDP与△POB中,
$\left\{\begin{array}{l}{DP=BO}\\{∠CPD=∠PBO}\\{PC=PB}\end{array}\right.$
∴△CDP≌△POB(SAS);
(2)解:①当四边形AOPD的AO边上的高等于半径时有最大面积,
(4÷2)×(4÷2) =2×2
=2×2
=4;
②如图:
∵DP∥AB,DP=BO,
∴四边形BPDO是平行四边形,
∵四边形BPDO是菱形,
∴PB=BO,
∵PO=BO,
∴PB=BO=PO,
∴△PBO是等边三角形,
∴∠PBA的度数为60°.
故答案为:4;60°.
点评 考查了菱形的判定,全等三角形的判定与性质,中位线的性质,解题的关键是SAS证明△CDP≌△POB.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
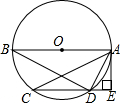 如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.
如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,射线PA切⊙O于点A,连接PO.
如图,射线PA切⊙O于点A,连接PO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
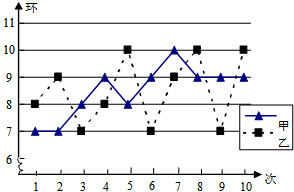 在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.
如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com