
【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
【答案】(1)k=-2(2)点B不在,点C在,(3)9<y<13
【解析】
试题分析:(1)把点A(2,3)代入y=kx+7即可求出k的值;(2)点B(-1,8),C(3,1)的横坐标代入函数解析式验证即可;(3)根据x的取值范围,即可求出y的取值范围.
试题解析:(1)把点A(2,3)代入y=kx+7得:k=-2
(2)当x=-1时,y=-2×(-1)+7=9
∵9≠8∴点B不在抛物线上.
当x=3时,y=-2×3+7=1
∴点C在抛物线上
(3)当x=-3时,y=13,当x=-,1时,y=9,所以9<y<13
考点:一次函数.
【题型】解答题
【结束】
24
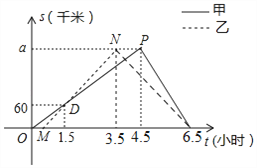
【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:

(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.
【答案】(1)甲、乙两车的速度分别为40km/h、60km/h,a的值是180km;(2)甲返回时的速度为90km/h
【解析】试题分析:(1)观察t轴,s轴表示的意义,利用v=![]() 求速度.(2) ,利用v=
求速度.(2) ,利用v=![]() 为等量列方程求解.
为等量列方程求解.
试题解析:
(1)由图象得:甲的速度为:60÷1.5=40(km/h),
乙的速度为:60÷(1.5﹣0.5)=60(km/h),
求a的方法如下:
方法1:由题意得: ![]() ﹣1﹣0.5,解得:a=180;
﹣1﹣0.5,解得:a=180;
方法2:设甲到达B地的时间为t时,则乙所用的时间为(t﹣1﹣0.5)时,
由题意得:40t=60(t﹣1﹣0.5),
t=4.5,
∴a=40t=40×4.5=180,
答:甲、乙两车的速度分别为40km/h、60km/h,a的值是180km.
(2)方法1:设甲返回时的速度为xkm/h,
则![]() ,
,
解得:x=90,
经检验:x=90是原方程的解,用符合题意,
所以,甲返回时的速度为90km/h;
方法2:甲、乙同时返回A地,则甲返回时所用的时间为: ![]() -1=2,
-1=2,
所以,甲返回时的速度为:180÷2=90(km/h).
图象如图所示:


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形①、②在直线上,正方形③如图放置,若正方形①、②的面积分别为81 cm2和144 cm2,则正方形③的边长为( )

A. 225 cm B. 63 cm C. 50 cm D. 15 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作试验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
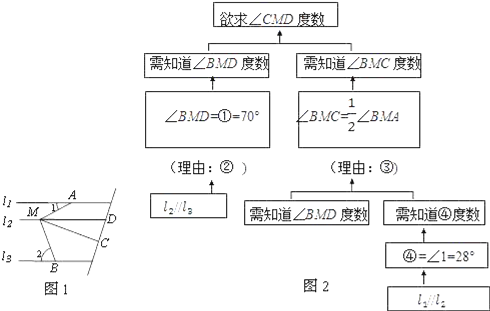
请问小坚的提示中①是∠ ,④是∠ .
理由②是: ;
理由③是: ;
∠CMD的度数是 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形. 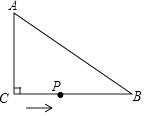
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com