
分析 本题是一道开放性的题,可根据平时经常见到的几种类型题:如行程问题,利润问题,工作量问题的模式进行编写.注意找好已知量,未知量.
解答 解:在列分式方程解应用题时:
(1)主要步骤有:①审清题意;②设未知数;③根据题意找 等量关系,列出分式方程;④解方程,并 检验;⑤写出答案;
故答案为:(1)等量,检验.
(2)为了帮助早收自然灾害的地区重建家园,某学校号召同学们自愿捐款.已知七年级同学捐款总额为4800元,八年级同学捐款总额为5000元,八年级捐款人数比七年级多20人,而且两个年级人均捐款额恰好相等.求七年级捐款人数.
解:如果设七年级捐款人数为x人,根据题意,得
$\frac{4800}{x}=\frac{5000}{x+20}$解得:x=480
经检验x=480是原方程的解.
答:七年级捐款人数为480人.
点评 本题为自列自解应用题,要注意所给方程的特点,根据自己的经验来列出应用题并解答.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
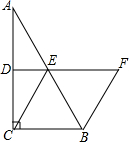 如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.
将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.
如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )| A. | y=6-$\frac{1}{2}$x(0<x<12) | B. | y=-$\frac{1}{2}$x2+6x(0<x<12) | ||
| C. | y=2x2-12x(0<x<12) | D. | y=$\frac{1}{2}$x2+6x(0<x<12) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-(y+z)2 | B. | (x-y)2-z2 | C. | -(x-y)2+z2 | D. | x2-(y-z)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
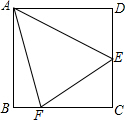 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com