A
分析:①根据BC=AC,∠ACB=90°可知∠CAB=∠ABC=45°,再由AD平分∠BAC可知∠BAE=∠EAF=22.5°,在Rt△ACD与Rt△BFC中,∠EAF+∠F=90°,∠FBC+∠F=90°,可求出∠EAF=∠FBC,由BC=AC可求出Rt△ADC≌Rt△BFC,故可求出AD=BF;
②由①中Rt△ADC≌Rt△BFC可直接得出结论;
③由①中Rt△ADC≌Rt△BFC可知,CF=CD,故AC+CD=AC+CF=AF,∠CBF=∠EAF=22.5°,在Rt△AEF中,∠F=90°-∠EAF=67.5°,根据∠CAB=45°可知,∠ABF=180°-∠EAF-∠CAB=67.5°,即可求出AF=AB,即AC+CD=AB;
④由③可知,△ABF是等腰三角形,由于BE⊥AD,故BE=

BF,在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF;
⑤由③可知,△ABF是等腰三角形,由于BE⊥AD,根据等腰三角形三线合一的性质即可解答.
解答:①∵BC=AC,∠ACB=90°,
∴∠CAB=∠ABC=45°,
∵AD平分∠BAC,
∴∠BAE=∠EAF=22.5°,
∵在Rt△ACD与Rt△BFC中,∠EAF+∠F=90°,∠FBC+∠F=90°,
∴∠EAF=∠FBC,
∵BC=AC,∠EAF=∠FBC,∠BCF=∠AEF,
∴Rt△ADC≌Rt△BFC,
∴AD=BF;
故①正确;
②∵①中Rt△ADC≌Rt△BFC,
∴CF=CD,
故②正确;
③∵①中Rt△ADC≌Rt△BFC,
∴CF=CD,AC+CD=AC+CF=AF,
∵∠CBF=∠EAF=22.5°,
∴在Rt△AEF中,∠F=90°-∠EAF=67.5°,
∵∠CAB=45°,
∴∠ABF=180°-∠F-∠CAB=180°-67.5°-45°=67.5°,
∴AF=AB,即AC+CD=AB,
故③正确;
④由③可知,△ABF是等腰三角形,
∵BE⊥AD,
∴BE=

BF,
∵在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,
故BE≠CF,
故④错误;
⑤由③可知,△ABF是等腰三角形,
∵BE⊥AD,
∴BF=2BE,
故⑤正确.
所以①②③⑤四项正确.
故选A.
点评:本题考查的是线段垂直平分线的性质及等腰三角形的判定与性质,熟知线段垂直平分线的性质及等腰三角形的判定与性质是解答此题的关键.

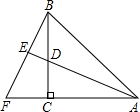 如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是
如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是 BF,在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF;
BF,在Rt△BCF中,若BE=CF,则∠CBF=30°,与②中∠CBF=22.5°相矛盾,故BE≠CF; BF,
BF,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为