
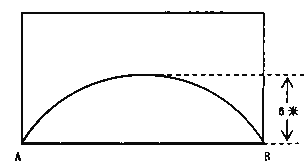
【题目】为了实现省城合肥跨越发展,近两年我市开始全面实施“畅通一环”工程,如图为一环路的一座下穿路拱桥,它轮廓是抛物线,桥的跨度AB=16米,拱高为6米.
(1)请以A点为坐标原点,AB所在直线为x轴建立平面直角坐标系,将抛物线放在直角坐标系中,求出抛物线的解析式;
(2)若桥拱下是双向行车道,其中一条行车道能否并排行驶宽3米,高2米的两辆汽车(汽车间隔不小于1米)说明理由
【答案】(1)建图见解析;y=![]() .(0≤x≤16);(2)不能,理由见解析.
.(0≤x≤16);(2)不能,理由见解析.
【解析】
(1)根据题目可知A、B,C的坐标,设出抛物线的解析式代入可求解;
(2)设DE是两辆车的宽度和,作EG垂直AB交抛物线于G,求出EG则可求解.
解:(1)以A点为坐标原点,AB所在直线为x轴建立平面直角坐标系,如图:
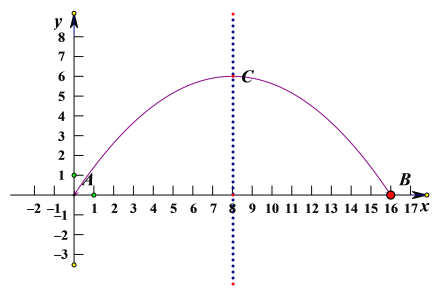
根据题目条件,A、B的坐标分别是(0,0)、(16,0)、顶点C的坐标是(8,6).
设抛物线的解析式y=a(x-8)2+6,将A的坐标代入得64a+6=0,
解得:a=![]() .
.
所以抛物线的表达式是y=![]() ;(0≤x≤16);
;(0≤x≤16);
(2)设DE是两辆车最内侧与最外侧的宽度和=3+1+3=7,AE=1,则E点坐标是(1,0),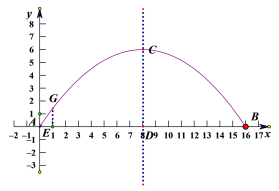
过E点作EG垂直AB交抛物线于G,则yH=![]() =
=![]() <2,
<2,
根据抛物线的特点,可知一条行车道不能并排行驶宽3米,高2米的两辆汽车(汽车间隔不小于1米).


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】甲乙两人同时登山,甲乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是 米/分钟,乙在A地提速时距地面的高度b为 米.
(2)若乙提速后,乙的速度是甲登山速度的3倍,请求出乙提速后y和x之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时乙距A地的高度为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
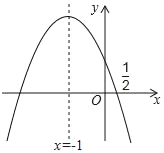
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
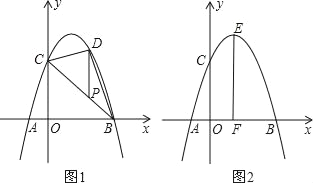
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
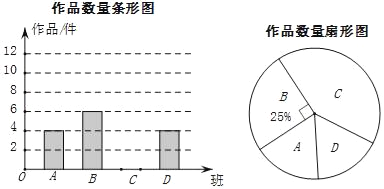
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
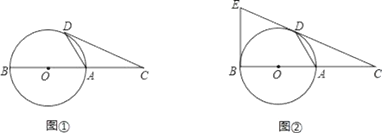
【题目】已知点C为直径BA的延长线上一点,CD切⊙O于点D,
(Ⅰ)如图①,若∠CDA=26°,求∠DAB的度数;
(Ⅱ)如图②,过点B作⊙O的切线交CD的延长线于点E,若⊙O的半径为3,BC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
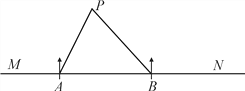
【题目】超速行驶是一种十分危险的违法驾驶行为,在一条东西走向的笔直高速公路MN上,小型车限速为每小时100千米. 现有一辆小汽车行驶到A处时,发现北偏东30°方向200米处有一超速监测仪P. 10秒后,小汽车行驶至B处,测得监测仪P在B处的北偏西45°方向上. 请问:这辆车超速了吗?通过计算说明理由.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com