
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上的一点,点E在BC边上,连接AE,DE,DC,AE=CD.
(1)求证:△ABE≌△CBD;
(2)若∠BAE=15°,求∠EDC的度数.

【答案】(1)证明见解析;(2)30°.
【解析】
(1)利用HL证明三角形全等即可;
(2)由直角三角形两锐角互余得到∠BEA的度数,再由全等三角形的性质得到∠BDC的度数,以及BD=BE,利用等腰直角三角形的性质求出∠BDE的度数,即可确定出∠EDC的度数.
(1)∵∠ABC=90°,D为AB延长线上一点,∴∠ABE=∠CBD=90°.
∵AB=CB,AE=CD,∴△ABE≌△CBD;
(2)∵∠BAE=15°,∴∠BEA=90°-15°=75°.
∵△ABE≌△CBD,∴∠BDC=∠BEA=75°,BE=BD.
∵∠DBC=90°,∴∠BDE=45°,∴∠EDC=75°﹣45°=30°.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD. 
(1)求证:△CDE∽△CAD;
(2)若AB=2,AC=2 ![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny. 据此判断下列等式成立的是(写出所有正确的序号)
①cos(﹣60°)=﹣ ![]() ;
;
②sin75°= ![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
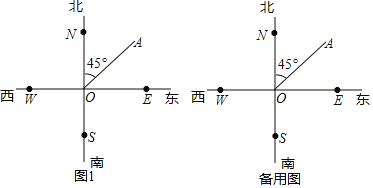
【题目】如图,射线ON,OE、OS、OW分别表示从点O出发的北、东、南、西四个方向,且点A在点O的北偏东45°方向上,点B在点O的北偏西30°方向上.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图中画出∠BOC;
(2)若OP是∠AOC的角平分线,请直接写出AOP的度数.(不需要写计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,M、N分别是BC与EF的中点,CF⊥AB,BE⊥AC.
(1)求证:MN⊥EF;
(2)连接FM、EM,若![]() ,试判断△FEM的形状.
,试判断△FEM的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
查看答案和解析>>
科目:初中数学 来源: 题型:
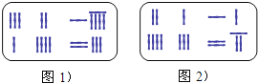
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OC为射线,OD、OE分别为∠AOC、∠BOC的平分线.
(1)判断射线OD、OE的位置关系,并说明理由;
(2)若∠AOD=30°,求证:OC为∠AOE的平分线;
(3)如果∠AOD:∠AOE=2:11,求∠BOE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com