

���� ��1���ɷ��е���ߵ�������4�ף���֪h=4����A��0��1�������������ʽ��
��2����y=0���ⷽ�̼��ɽ�����⣻
��3����x=13-3=10����y=-$\frac{1}{12}$��x-6��2+4�����ɵõ����ۣ�
��4����ͼ�ɵõڶ���������ľ���ΪCD���������֪CD=EF���Ӷ��÷���-$\frac{1}{12}$��x-6��2+4=2���x��ֵ���ɵõ����ۣ�
��� �⣺��1���ٵ�h=4ʱ��y=a��x-6��2+4����A��0��1��
��1=a��0-6��2+4��
��a=-$\frac{1}{12}$��
��y=-$\frac{1}{12}$��x-6��2+4��
��2����y=0����0=-$\frac{1}{12}$��x-6��2+4����ã�x1=4$\sqrt{3}$+6��13��x2=-4$\sqrt{3}$+6��0����ȥ��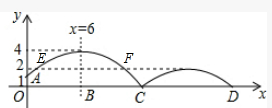
������е���Զˮƽ������13�ף�
��3����x=13-3=10ʱ��y=$\frac{8}{3}$��1.7+0.3=2��
��������Ա����������
��4����ͼ������ڶ��ε�����ľ���ΪCD��
��������֪CD=EF�����൱�ڽ�������AEMFC����ƽ����2����λ����
��-$\frac{1}{12}$��x-6��2+4=2��
��ã�x1=6-2$\sqrt{6}$��x2=6+2$\sqrt{6}$��
��CD=x2-x1=4$\sqrt{6}$��10��
��������ᵯ��10�ף�
���� ������Ҫ�����˶��κ�����ʵ��Ӧ�ã�Ū�����⣬���ν�ϣ��Ѻ�������ת��Ϊ���̻�ʽ�����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��C��D���߶�AB�ֳ�2��3��4�����֣�E��F�ֱ���AC��BD���е㣬��AB=36����EF�ij���
��ͼ��C��D���߶�AB�ֳ�2��3��4�����֣�E��F�ֱ���AC��BD���е㣬��AB=36����EF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����С���ң�ͼ�е�O����ѧУ���ڵصļ�ͼ����֪OA=2cm��OB=2.5cm��OP=4cm��CΪOP���е㣮
��ͼ����С���ң�ͼ�е�O����ѧУ���ڵصļ�ͼ����֪OA=2cm��OB=2.5cm��OP=4cm��CΪOP���е㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com