
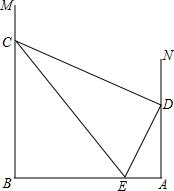
 ��ͼ�����߶�AB���˵�ֱ���MB��AB��NA��AB������ֱ�Ϊ��B����A����D������AN�ϵ�-�㣬��E���߶�AB�ϵ�һ���㣬����DE������D��DC��DE��������BM���ڵ�C������CE��
��ͼ�����߶�AB���˵�ֱ���MB��AB��NA��AB������ֱ�Ϊ��B����A����D������AN�ϵ�-�㣬��E���߶�AB�ϵ�һ���㣬����DE������D��DC��DE��������BM���ڵ�C������CE������ ��1�����ȹ�D��DF��AN�ڵ�F���жϳ��ı���BADF�Ǿ��Σ������Ƶ�FD=AB��Ȼ��������������Ƶ��ж��������жϳ���CDF�ס�EDA�������Ƶ�$\frac{DE}{DC}=\frac{AD}{FD}$���ٸ���FD=AB���жϳ�$\frac{DE}{DC}$=$\frac{AD}{AB}$���ɣ�
��2�����ȸ���AD=4��AB=8��$\frac{DE}{DC}$=$\frac{AD}{AB}$���жϳ�$\frac{DE}{DC}=\frac{1}{2}$����DE=x����DC=2x����Rt��CDE�У��ɹ��ɶ��������DE��ֵ�Ƕ��٣�Ȼ����Rt��ADE�У����ݹ��ɶ��������AE��ֵ�Ƕ��ټ��ɣ�
��3��������CG��AN�ڵ�G����AD=x��AB=y����BC=2x��Ȼ��ֱ������DCE��������Լ���BCE����ADE������ͣ�Ȼ����ݡ�DCE���ı���ABCD�����֮����2��5���ɵá�DCE��������BCE����ADE������͵ı���2��3�����x��y��ֵ���������sin��DCE��ֵ�Ƕ��ټ��ɣ�
��� ��1��֤������ͼ1����D��DF��AN�ڵ�F��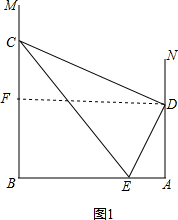 ��
��
��MB��AB��NA��AB��DF��AN��
���ı���BADF�Ǿ��Σ�
��FD=AB����FDE+��EDA=90�㣬
��DC��DE��
���CDF+��FDE=90�㣬
���CDF=��EDA��
�ڡ�CDF�͡�EDA�У�
$\left\{\begin{array}{l}{��CFD=��EAD=90��}\\{��CDF=��EDA}\end{array}\right.$
���CDF�ס�EDA��
��$\frac{DE}{DC}=\frac{AD}{FD}$��
�֡�FD=AB��
��$\frac{DE}{DC}$=$\frac{AD}{AB}$��
��2����ͼ2��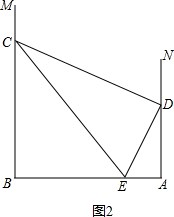 ��
��
��AD=4��AB=8��$\frac{DE}{DC}$=$\frac{AD}{AB}$��
��$\frac{DE}{DC}=\frac{1}{2}$��
��DE=x����DC=2x��
��DC��DE��CE=10��
�ɹ��ɶ������ɵã�x2+��2x��2=102��
��ã�x=2$\sqrt{5}$��x=-2$\sqrt{5}$����ȥ����
��DE=2$\sqrt{5}$��
��Rt��ADE��AE=$\sqrt{E{D}^{2}-D{A}^{2}}$=$\sqrt{��2\sqrt{5}��^{2}-{4}^{2}}$=2��
�൱AE=2ʱ���߶�CE�ij�ǡ��Ϊ10��
��3����ͼ3����CG��AN�ڵ�G��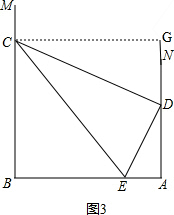 ��
��
��MB��AB��NA��AB��CG��AN��
���ı���BAGC�Ǿ��Σ�
��AG=BC��CG=AB��
��BC=2AD��
����AD=x��AB=y����BC=2x��
��DG=AG-AD=BC-AD=2x-x=x��
��CD=$\sqrt{{x}^{2}{+y}^{2}}$��
�ɣ�1�����ɵ�$\frac{DE}{DC}$=$\frac{AD}{AB}$��
��$\frac{x}{y}=\frac{DE}{\sqrt{{x}^{2}{+y}^{2}}}$��
��DE=$\frac{x\sqrt{{x}^{2}{+y}^{2}}}{y}$��
��S��DCE=$\frac{1}{2}$DE•CD=$\frac{1}{2}$��$\frac{x\sqrt{{x}^{2}{+y}^{2}}}{y}$��$\sqrt{{x}^{2}{+y}^{2}}$=$\frac{x}{2y}$��x2+y2����
��DE=$\frac{x\sqrt{{x}^{2}{+y}^{2}}}{y}$��AD=x��
��AE=$\sqrt{{DE}^{2}{-AD}^{2}}$=$\sqrt{\frac{{x}^{2}{��x}^{2}{+y}^{2}��}{{y}^{2}}{-x}^{2}}$=$\frac{{x}^{2}}{y}$��
�֡�AB=y��
��BE=y-$\frac{{x}^{2}}{y}$=$\frac{{y}^{2}{-x}^{2}}{y}$��
��S��BCE+S��ADE=$\frac{1}{2}��2x$��$\frac{{y}^{2}{-x}^{2}}{y}$+$\frac{1}{2}$��$\frac{{x}^{2}}{y}$��x=$\frac{2{xy}^{2}{-x}^{3}}{2y}$��
�֡ߡ�DCE���ı���ABCD�����֮����2��5��
��$\frac{x}{2y}$��x2+y2����$\frac{2{xy}^{2}{-x}^{3}}{2y}$=2��3��
�������ɵ�
��x2+y2������2y2-x2��=2��3��
��5x2=y2��
��$\frac{x}{y}=\frac{1}{\sqrt{5}}$��
��$\frac{DE}{DC}=\frac{1}{\sqrt{5}}$��
��sin��DCE=$\frac{DE}{CE}=\frac{1}{\sqrt{{1}^{2}{+��\sqrt{5}��}^{2}}}$=$\frac{\sqrt{6}}{6}$��
���� ��1��������Ҫ���������������Ƶ��ж������ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ�������߷��������Ӧ�ߵı���ȵ��������������ƣ���������нǷ��������Ӧ�ߵı�����ҼнǶ�Ӧ��ȵ��������������ƣ������Ƿ���������Ƕ�Ӧ��ȵ��������������ƣ�
��2����������˹��ɶ�����Ӧ�ã������ε���������Լ����Ǻ���ֵ����Ҫ�������գ�


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꼪��ʡ���꼶��ѧ��������ѧģ���Ծ����ģ��������棩 ���ͣ������
��a2+b2��2a+4b+5=0����2a+b=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
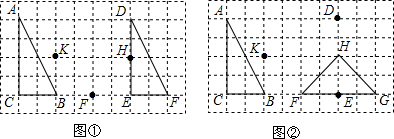
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
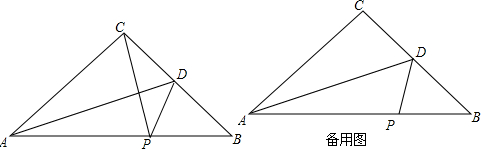
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
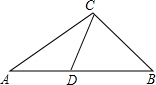 ��ͼ����D�ڡ�ABC�ı�AB�ϣ���AC2=AB•AD�������и�ʽ��һ���������ǣ�������
��ͼ����D�ڡ�ABC�ı�AB�ϣ���AC2=AB•AD�������и�ʽ��һ���������ǣ�������| A�� | ��ABC=��ACD | B�� | $\frac{BC}{AC}$=$\frac{CD}{AD}$ | C�� | $\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$ | D�� | ��A=��BCD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
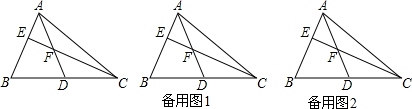
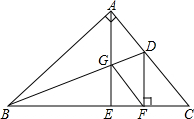 ��ͼ���ڡ�ABC�У���BAC=90�㣬��BC�Ͻ�ȡBF=BA����DF��BC��AC��D�㣬AE��BC��E�㣬��BD��G�㣬����GF����֤��DGƽ�֡�AGF��
��ͼ���ڡ�ABC�У���BAC=90�㣬��BC�Ͻ�ȡBF=BA����DF��BC��AC��D�㣬AE��BC��E�㣬��BD��G�㣬����GF����֤��DGƽ�֡�AGF���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com