
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
【答案】
(1)证明:∵在ABCD中,AB=CD,
∴BC=AD,∠ABC=∠CDA.
又∵BE=EC= ![]() BC,AF=DF=
BC,AF=DF= ![]() AD,
AD,
∴BE=DF.
∴△ABE≌△CDF.
(2)解:∵四边形AECF为菱形时,
∴AE=EC.
又∵点E是边BC的中点,
∴BE=EC,即BE=AE.
又BC=2AB=4,
∴AB= ![]() BC=BE,
BC=BE,
∴AB=BE=AE,即△ABE为等边三角形,
ABCD的BC边上的高为2×sin60°= ![]() ,
,
∴菱形AECF的面积为2 ![]() .
.

【解析】第(1)问要证明三角形全等,由平行四边形的性质,很容易用SAS证全等.第(2)要求菱形的面积,在第(1)问的基础上很快知道△ABE为等边三角形.这样菱形的高就可求了,用面积公式可求得.考查了全等三角形,四边形的知识以及逻辑推理能力.(1)用SAS证全等;(2)若四边形AECF为菱形,则AE=EC=BE=AB,所以△ABE为等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个饭店所有员工的月收入情况如下:

你认为用来描述该饭店员工的月收入水平不太恰当的是( )
A. 所有员工月收入的平均数
B. 所有员工月收入的中位数
C. 所有员工月收入的众数
D. 所有员工月收入的中位数或众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() ,把一条长为2016个单位长度且没有弹性的细线
,把一条长为2016个单位长度且没有弹性的细线![]() 线的粗细忽略不计
线的粗细忽略不计![]() 的一端固定在点A处,并按
的一端固定在点A处,并按![]() 的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是![]()
![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.
(1)a=![]() ,b=2
,b=2![]() ,c=
,c=![]() ;
;
(2)a=5,b=7,c=9;
(3)a=2,b=![]() ,c=
,c=![]() ;
;
(4)a=5,b=2![]() ,c=1.
,c=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下条件不能判别四边形ABCD是矩形的是( )
A. AB=CD,AD=BC,∠A=90° B. OA=OB=OC=OD
C. AB=CD,AB∥CD,AC=BD D. AB=CD,AB∥CD,OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形OABC中,OA=3,AB=6,以OA,OC所在的直线为坐标轴,建立如图1的平面直角坐标系.将矩形OABC绕点O顺时针方向旋转,得到矩形ODEF,当点B在直线DE上时,设直线DE和x轴交于点P,与y轴交于点Q.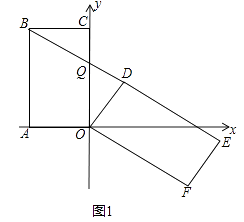
(1)求证:△BCQ≌△ODQ;
(2)求点P的坐标;
(3)若将矩形OABC向右平移(图2),得到矩形ABCG,设矩形ABCG与矩形ODEF重叠部分的面积为S,OG=x,请直接写出x≤3时,S与x之间的函数关系式,并且写出自变量x的取值范围.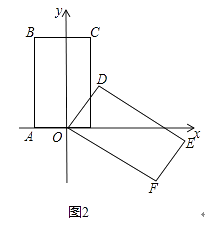
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com