
 在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.分析 ①作OF⊥AB交AB于F,交圆于G,连接OA,根据垂径定理求出AF的长,根据勾股定理求出OF,计算即可;
②连接OC,根据垂径定理求出CE的长,根据勾股定理求出答案.
解答 解: ①作OF⊥AB交AB于F,交圆于G,连接OA,
①作OF⊥AB交AB于F,交圆于G,连接OA,
∴AF=$\frac{1}{2}$AB=8,
由勾股定理得,OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=15,
则GF=OG-OF=2dm;
②连接OC,
∵OE⊥CD,
∴CE=$\frac{1}{2}$EF=15,
OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=8,
则EF=OG-OE-FG=7dm,
答:油的最大深度上升了7dm.
点评 本题考查的是垂径定理和勾股定理的应用,平分弦垂直于弦的直径平分弦,并且平分弦所对的两条弧.垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.


科目:初中数学 来源: 题型:解答题
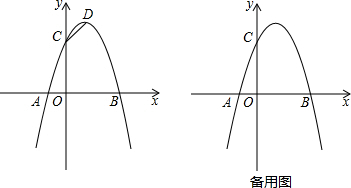
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-2)与|-2| | B. | (-2)2与-22 | C. | -2与$\frac{1}{2}$ | D. | -(-2)与$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
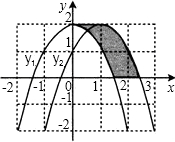 如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2,回答下列问题:
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com