
 王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
王杰为了测量他家小楼附近楼房AB的高度,他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°,又测得两幢楼之间的距离BC为10$\sqrt{3}$m.(以下计算结果精确到0.1m,参考值$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)分析 (1)通过解Rt△BCD得出CD=BC•tan30°,求得答案即可;
(2)由图可知:AB=AF+DE+CD,利用直角三角形的性质和锐角三角函数的意义求得AF,得出答案即可.
解答 解:(1)在Rt△BCD中,∠CBD=30°,BC=10$\sqrt{3}$m,
∴CD=BC•tan30°,
∴CD=10(m).
答:王杰家的楼房CD的高是10m;
(2)在Rt△AFE中,
∵∠AEF=45°,
∴AF=EF=BC=10$\sqrt{3}$m,
∴AB=AF+DE+CD=28.9(m).
答:楼房AB的高度是28.9m.
点评 本题考查了解直角三角形的应用,题目中涉及到了仰俯角和坡度角的问题,解题的关键是构造直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
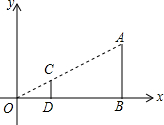 在直角坐标系中有两点A(6,3)、B(6,0).以原点O为位似中心,把线段AB按相似的1:3缩小后得到线段CD,点C在第一象限(如图),则点C的坐标为(2,1).
在直角坐标系中有两点A(6,3)、B(6,0).以原点O为位似中心,把线段AB按相似的1:3缩小后得到线段CD,点C在第一象限(如图),则点C的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 领口尺寸(单位:cm) | 38 | 39 | 40 | 41 | 42 |
| 件数 | 1 | 5 | 3 | 3 | 2 |
| A. | 39cm、39cm | B. | 39cm、39.5cm | C. | 39cm、40cm | D. | 40cm、40cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
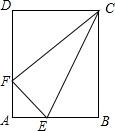 如图,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处,如果$\frac{AB}{BC}=\frac{3}{4}$,那么tan∠DCF=$\frac{\sqrt{7}}{3}$.
如图,将矩形ABCD沿CE折叠,点B恰好落在边AD上的点F处,如果$\frac{AB}{BC}=\frac{3}{4}$,那么tan∠DCF=$\frac{\sqrt{7}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
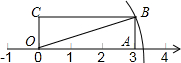 如图所示,矩形OABC的边长OA长为3,边AB长为1,OA在数轴上,以O为圆心,OB为半径画弧,交正半轴于一点,则这个点表示的实数是( )
如图所示,矩形OABC的边长OA长为3,边AB长为1,OA在数轴上,以O为圆心,OB为半径画弧,交正半轴于一点,则这个点表示的实数是( )| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 3.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com