
【题目】如图,已知![]() 、
、![]() 与⊙
与⊙![]() 相切于点
相切于点![]() 、
、![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .若
.若![]() ,
,![]() .
.
(![]() )求⊙
)求⊙![]() 的半径
的半径![]() .
.
(![]() )求
)求![]() 的长.
的长.
【答案】(1)3;(2)![]() .
.
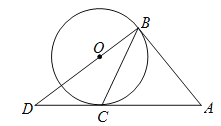
【解析】试题分析:(1)连接半径OA,在Rt△OCD中,根据勾股定理列方程可求得r的值;
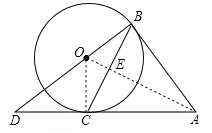
(2)由垂直平分线的逆定理得:OA是BC的中垂线,根据垂径定理得:BE=CE,最后利用面积法列式可求得BE的长,由BC=2BE即可得到结论.
试题解析:解:(1)连接OC.∵AB、AC是⊙O的切线,∴AB=AC=6,OC⊥AD,BD⊥AB,∴∠ABD=∠OCD=90°,在Rt△ABD中,由勾股定理得:AD=![]() =10,∴CD=10﹣6=4.∵⊙O的半径r,∴OB=OC=r,OD=8﹣r,在Rt△OCD中,(8﹣r)2=r2+42,64﹣16r=16,∴r=3;
=10,∴CD=10﹣6=4.∵⊙O的半径r,∴OB=OC=r,OD=8﹣r,在Rt△OCD中,(8﹣r)2=r2+42,64﹣16r=16,∴r=3;
(2)连接OA,交BC于E.∵AB=AC,OB=OC,∴OA是BC的中垂线,∴BE=CE,在Rt△ABO中,AO=![]() =
=![]() ,∴S△ABO=
,∴S△ABO=![]() ABOB=
ABOB=![]() OABE,6×3=
OABE,6×3=![]() BE,∴BE=
BE,∴BE=![]() ,∴BC=2BE=
,∴BC=2BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△ABC关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角形的直角顶点0按图1方式叠放在一起(其中∠C=30°,∠CDO=60°;∠OAB=∠OBA=45°).△COD绕着点O顺时针旋转一周,旋转的速度为每秒10°,若旋转时间为t秒,请回答下列问题:(请直接写出答案)
(1)当0<t<9时(如图2),∠BOC与∠AOD有何数量关系
(2)当t为何值时,边OA∥CD?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
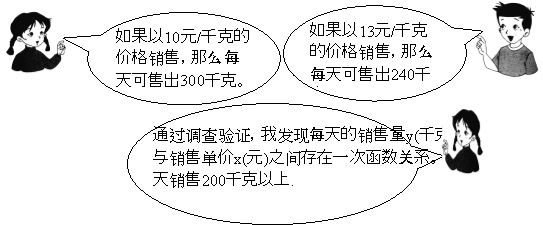
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式。(6分)
(2)该超市销售这种水果每天获取的利润为1040元,那么销售单价为多少元?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
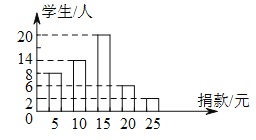
【题目】在“爱满金陵”慈善一日捐活动中,学校团总支为了了解本校写生的捐款情况,随机抽取了![]() 名学生的捐款数进行了统计,并绘制成统计图.
名学生的捐款数进行了统计,并绘制成统计图.
(![]() )这
)这![]() 名同学捐款的众数为__________元,中位数为__________.
名同学捐款的众数为__________元,中位数为__________.
(![]() )求这
)求这![]() 名同学捐款的平均数.
名同学捐款的平均数.
(![]() )该校共有
)该校共有![]() 名学生参与捐款,请估计该校学生的捐款总数.
名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试成绩在总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试成绩在总人数的前90%为合格,该校初二年级有800名学生,求全年级生物合格的学生共约多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.
(1)求证:OE=OF;
(2)连接BE、DF,若BD平分∠EBF,试判断四边形EBFD的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com