
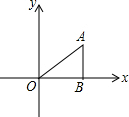 如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
如图,在△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )| A. | (-1,-$\sqrt{3}$) | B. | (-1,-$\sqrt{3}$)或(-2,0) | C. | (-$\sqrt{3}$,1)或(0,-2) | D. | (-$\sqrt{3}$,1) |
分析 需要分类讨论:在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标.
解答 解:∵△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,
∴tan∠AOB=$\frac{AB}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,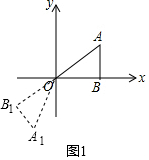
则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-1,-$\sqrt{3}$);
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,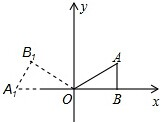
则∠A1OC=150°-∠AOB-∠BOC=150°-30°-90°=30°,
则易求A1(-2,0);
综上所述,点A1的坐标为(-1,-$\sqrt{3}$)或(-2,0).
故选:B.
点评 本题考查了坐标与图形变化-旋转.解题时,注意分类讨论,以防错解.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
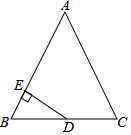 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )| A. | $\frac{10}{13}$ | B. | $\frac{15}{13}$ | C. | $\frac{45}{13}$ | D. | $\frac{60}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
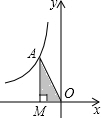 如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10.
如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{24}{3}$ | B. | -$\frac{2}{{3}^{4}}$ | C. | -($\frac{2}{3}$)4 | D. | (-$\frac{2}{3}$)4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
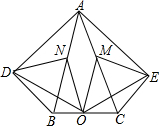 在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.
在五边形ADBCE中,∠ADB=∠AEC=90°,∠DAB=∠EAC,M、N、O分别为AC、AB、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com