
 定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.
定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$. 分析 分两种情况:①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可.
解答 解:分两种情况:
①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}-A{M}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$;
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}+A{M}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$;
综上所述:BN的长为$\sqrt{5}$或$\sqrt{13}$.
故答案为:$\sqrt{3}$或$\sqrt{15}$.
点评 本题考查了新定义“勾股分割点”、勾股定理;理解新定义,熟练掌握勾股定理,进行分类讨论是解决问题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,点M、N是线段AB的勾股分割点(勾股分割点定义:指M、N把线段AB分割成AM,MN,和BN.若以AM,MN,和BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点).现若已知AM=3,MN=4,则BN=5或$\sqrt{7}$.
如图,点M、N是线段AB的勾股分割点(勾股分割点定义:指M、N把线段AB分割成AM,MN,和BN.若以AM,MN,和BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点).现若已知AM=3,MN=4,则BN=5或$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 乘法分配律 | B. | 乘法结合律 | ||
| C. | 乘法交换律 | D. | 乘法结合律和交换律 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
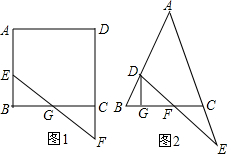 (1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.
(1)如图1,E、F是正方形ABCD的边AB及DC延长线上的点,且BE=CF,则BG与BC的数量关系是BG=$\frac{1}{2}$BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一次函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,则化简:$\sqrt{(n-m)^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为( )
一次函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,则化简:$\sqrt{(n-m)^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为( )| A. | -2n+3 | B. | -2m+3 | C. | m-3 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com