
分析 (1)设统景镇去年柑橘和蔬菜的收成各是x,y吨,然后列出方程组求解即可;
(2)设安排甲车x辆,表示出安排乙车(33-x),然后根据运送蔬菜和水果的袋数列出不等式组求解,再根据x是正整数确定运送方案;
(3)表示出运输费用,然后根据一次函数的增减性确定运输费最少的方案即可.
解答 解:(1)设统景镇去年柑橘和蔬菜的收成各是x,y吨,
根据题意得,$\left\{\begin{array}{l}{x+y=420-80}\\{20%x+30%y=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=220}\\{y=120}\end{array}\right.$,
答:统景镇去年柑橘的收成是220吨,蔬菜的收成是120吨;
(2)∵220(1+20%)=264吨,120(1+30%)=156吨,
设安排甲车a辆,则安排乙车(33-a),
根据题意得$\left\{\begin{array}{l}{13a+5(33-a)≥264}\\{3a+6(33-a)≥156}\end{array}\right.$,
解得:12$\frac{3}{8}$≤a≤14,
∵车的辆数x是正整数,
∴x=13、44,
∴设计方案有两种:
方案一:甲车13辆,乙车20辆,
方案二:甲车14辆,乙车19辆;
(3)运输费用W=600x+500(33-x)=100x+16500,
∵k=100>0,
∴W随x的增大而增大,
∴x=13时,运输费用最少,最少运输费=100×13+16500=17800元.
答:安排13辆甲车,20辆乙车运费最少,最少为17800元.
点评 本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用,读懂题目信息,准确确定出等量关系和不等量关系分别列出方程组和不等式组是解题的关键,也是本题的难点.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )
如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )| A. | AC⊥BD | B. | AB=BC | C. | AC=BD | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
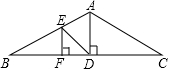 如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com