
| A. | x-2=1 | B. | x+2=1 | C. | x+2=-1 | D. | x-2=-1 |
科目:初中数学 来源: 题型:选择题
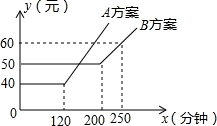 如图,某电信公司提供了一个月使用移动通讯工具的A,B两种方案的通讯费用y(元)与通话时间x(元)之间的关系,下面给出了关于A、B两种方案的看法:
如图,某电信公司提供了一个月使用移动通讯工具的A,B两种方案的通讯费用y(元)与通话时间x(元)之间的关系,下面给出了关于A、B两种方案的看法:| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
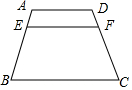 在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )
在梯形ABCD中,EF∥AD∥BC,要使梯形AEFD∽梯形EBCF,则应满足的条件是( )| A. | EF=$\frac{1}{2}$BC | B. | EF2=AD•BC | C. | AE=EB | D. | $\frac{AE}{AB}$=$\frac{AD}{EF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上A、B两点分别对应实数a、b,有如下4个结论①a<b,②|a|>|b|,③a+b>0,④a-b>0,则正确的结论有( )个.
如图,数轴上A、B两点分别对应实数a、b,有如下4个结论①a<b,②|a|>|b|,③a+b>0,④a-b>0,则正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
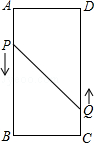 如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com