Question

17．（1）如图1，在AB直线一侧C、D两点，在AB上找一点P，使C、D、P三点组成的三角形的周长最短，找出此点并说明理由．
（2）如图2，在∠AOB内部有一点P，是否在OA、OB上分别存在点E、F，使得E、F、P三点组成的三角形的周长最短，找出E、F两点，并说明理由．
（3）如图3，在∠AOB内部有两点M、N，是否在OA、OB上分别存在点E、F，使得E、F、M、N，四点组成的四边形的周长最短，找出E、F两点，并说明理由．

Answer 1

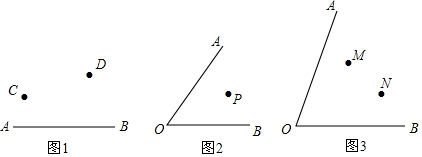
分析 （1）由于△PCD的周长=PC+CD+PD，而CD是定值，故只需在直线l上找一点P，使PC+PD最小．如果设C关于l的对称点为C′，使PC+PD最小就是使PC′+PD最小；
（2）作P关于OA、OB的对称点C、D，连接CD角OA、OB于E、F．此时△PEF周长有最小值；
（3）如图3，作M关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F，此时使得E、F、M、N，四点组成的四边形的周长最短．

解答 解：（1）如图1，作C关于直线AB的对称点C′，
连接C′D交AB于点P．
则点P就是所要求作的点．
理由：在l上取不同于P的点P′，连接CP′、DP′．
∵C和C′关于直线l对称，
∴PC=PC′，P′C=P′C′，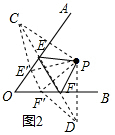
而C′P+DP＜C′P′+DP′，
∴PC+DP＜CP′+DP′
∴CD+CP+DP＜CD+CP′+DP′
即△CDP周长小于△CDP′周长；
（2）如图2，作P关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F，
则点E，F就是所要求作的点，
理由：在OA，OB上取不同于E，F的点E′，F′，连接CE′、E′P，
∵C和P关于直线OA对称，
∴PE=CE，CE′=PE′，PF=DF，PF′=DF′，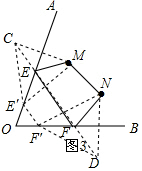
∵PE+EF+PF=CE+EF+DF，PE′+PF′+E′F′=CE′+E′F′+DF′，
∴CE+EF+DF＜CE′+E′F′+DF′，
∴PE+EF+PF＜PE′+E′F′+PF′；
（3）如图3，作M关于OA的对称点C，作N关于OB的对称点D，连接CD，交OA于E，OB于F，
则点E，F就是所要求作的点．
理由：在OA，OB上取不同于E，F的点E′，F′，连接CE′、E′F′，DF′，
∵C和M关于直线OA对称，
∴ME=CE，CE′=ME′，NF=DF，NF′=DF′，
由（2）得知MN+ME+EF+NF＜MN+ME′+E′F′+F′D．

点评 此题主要考查了平面内最短路线问题求法以及垂直平分线的性质等知识，根据已知得出对称点的位置是解题关键．