
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)如果AB=12,BC=15,求tan∠FBE的值.

【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)由矩形的性质推知∠A=∠D=∠C=90°.然后根据折叠的性质,等角的余角相等推知∠ABF=∠DFE,易证得△ABE∽△DFE;
(2)由勾股定理求得AF=9,得出DF=6,由△ABF∽△DFE,求得EF=7.5,由三角函数定义即可得出结果.
试题解析:(1)∵四边形ABCD是矩形.
∴∠A=∠D=∠C=90°,AD=BC,
∵△BCE沿BE 折叠为△BFE.
∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∠AFB十∠ABF=90°,
∴∠ASF=∠DFE,
∴△ABF∽△DFE.
(2)由折叠的性质得:BF=BC=15,
在Rt△ABF中,由勾股定理求得AF=![]() ,
,
∴DF=AD﹣AF=6,
∵△ABF∽△DFE,
∴![]() ,
,
即![]() ,
,
解得:EF=7.5,
∴tan∠FBE=![]() .
.


科目:初中数学 来源: 题型:
【题目】正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )
A. k≥2 B. k≤2 C. k>2 D. k<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
(x+1)(x﹣3)与x轴交于A、B两点,与y轴交于点C,点D为该抛物线的对称轴上一点,当点D到直线BC和到x轴的距离相等时,则点D的坐标为 .
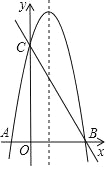
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P关于x轴的对称点P1的坐标是(2,3),那么点P关于原点的对称点P2的坐标是( )
A.(﹣3,﹣2)
B.(2,﹣3)
C.(﹣2,﹣3)
D.(﹣2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.表是甲班和乙班成绩最好的5名学生的比赛成绩.
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)甲班的优秀率为60%,则乙班的优秀率为 ;
(2)甲班比赛成绩的方差S甲2=![]() ,求乙班比赛成绩的方差;
,求乙班比赛成绩的方差;
(3)根据以上信息,你认为应该把团体第一名的奖状给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对0.05049分别取近似值,其中错误的是( )
A、0.1(精确到0.1)B、0.05(精确到百分位)
C、0.05(精确到千分位)D、0.050(精确到0.001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门. ![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com