在等腰△ABC中,CD是底边AB上的高,E是腰BC的中点,AE与CD交于F,现给出三条路线:
(a)A→F→C→E→B→D→A;
(b)A→C→E→B→D→F→A;
(c)A→D→B→E→F→C→A;
它们的长度分别记为L(a)、L(b)及L(c),则L(a)<L(b),L(a)<L(c),L(b)<L(c)中一定能成立的是________.
L(a)<L(b)
分析:根据题意可以得到F是△ABC的重心.从而得到CF=2DF,AF=2EF,AF=BF,利用L(a)=AF+FC+CB+BA、L(c)=AB+BE+EF+FC+CA得到L(c)-L(a)=(AB-BD)+(EF-FA)+(FC-DF)-CE=AD+DF-CE-EF,所以当△ABC为等边三角形时,AD=CE,DF=EF,此时有L(a)-L(b)=FC+DA-AC-DF=DF+DA-AC由于当∠ACB较大时,AC与AD可以很接近,取CD足够长可使L(a)>L(b),结论得出.
解答:依题意,知F是△ABC的重心.
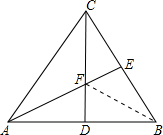
∴CF=2DF,AF=2EF,AF=BF,
∵L(a)=AF+FC+CB+BA
L(c)=AB+BE+EF+FC+CA
∴L(c)-L(a)=(AB-BD)+(EF-FA)+(FC-DF)-CE=AD+DF-CE-EF
当△ABC为等边三角形时,AD=CE,DF=EF,此时有L(a)-L(b)=FC+DA-AC-DF=DF+DA-AC由于当∠ACB较大时,AC与AD可以很接近,取CD足够长可使L(a)>L(b),如取∠ACB=120°,AC=BC=1,则AD=

∴L(a)-L(b)=
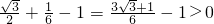
故L(a)<L(b)不恒成立.
故答案为L(a)<L(b).
点评:本题考查了几何不等式及三角形的重心的知识,在中学阶段重心涉及较少,因此本题属于一道难题.



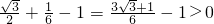 故L(a)<L(b)不恒成立.
故L(a)<L(b)不恒成立.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案 (2013•闸北区二模)如图,在等腰△ABC中,底边BC的中点是点D,底角的正切值是
(2013•闸北区二模)如图,在等腰△ABC中,底边BC的中点是点D,底角的正切值是 如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,
如图,在等腰△ABC中,∠ABC=90°,D为底边AC中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=12,FC=5,