
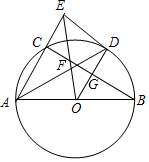
 如图,AB为⊙O的直径,AC为弦,∠BAC的平分线交⊙O于D,过D作⊙O的切线交AC的延长线于E,OE交AD于F.
如图,AB为⊙O的直径,AC为弦,∠BAC的平分线交⊙O于D,过D作⊙O的切线交AC的延长线于E,OE交AD于F.分析 (1)由条件可证明OD∥AE,结合切线的性质可求得∠AED=90°,可证明DE⊥AE;
(2)设AC=3k,AB=5k,BC=4k,可证OD垂直平分BC,利用勾股定理可得到OG,得到DG,于是AE=4k,然后通过OD∥AE,利用相似比即可求出$\frac{DF}{AF}$的值.
解答 (1)证明:
∵OD=OA,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∴∠ODA=∠ODA,
∴OD∥AE,
∵DE为⊙O的切线,
∴OD⊥DE,
∴DE⊥AE;
(2)解:
∵AB为直径,
∴∠ACB=90°,
又∵OD∥AE,
∴∠OGB=∠ACB=90°,
∴OD⊥BC,
∴G为BC的中点,即BG=CG,
又∵$\frac{AC}{AB}$=$\frac{3}{5}$,
∴设AC=3k,AB=5k,根据勾股定理得:BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4k,
∴OB=$\frac{1}{2}$AB=$\frac{5}{2}$k,BG=$\frac{1}{2}$BC=2k,
∴OG=$\sqrt{O{B}^{2}-B{G}^{2}}$=$\frac{3}{2}$k,
∴DG=OD-OG=$\frac{5}{2}$k-$\frac{3}{2}$k=k,
又∵四边形CEDG为矩形,
∴CE=DG=k,
∴AE=AC+CE=3k+k=4k,
而OD∥AE,
∴$\frac{FD}{AF}$=$\frac{OD}{AE}$=$\frac{\frac{5}{2}k}{4k}$=$\frac{5}{8}$.
点评 本题主要考查了切线的判定定理,能够综合运用角平分线的性质以及平行线分线段成比例定理是解题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
 如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=40m,则A、B两点间的距离是( )
如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=40m,则A、B两点间的距离是( )| A. | 20m | B. | 80m | C. | 120m | D. | 160m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,以∠AOB的顶点为圆心,取适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )
如图,以∠AOB的顶点为圆心,取适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是( )| A. | 射线OE是∠AOB的平分线 | B. | O、E两点关于CD所在直线对称 | ||
| C. | △COD是等腰三角形 | D. | C、D两点关于OE所在直线对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2和-7 | B. | 1.2和7 | C. | 0.12和-7 | D. | 0.12和-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com