
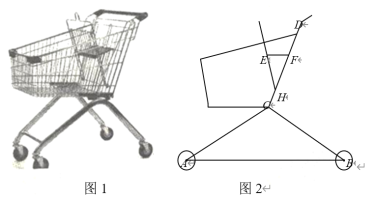
【题目】如图1是超市的手推车,如图2是其侧面示意图,已知前后车轮半径均为5 cm,两个车轮的圆心的连线AB与地面平行,测得支架AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,CD=50cm.
(1)求扶手前端D到地面的距离;
(2)手推车内装有简易宝宝椅,EF为小坐板,打开后,椅子的支点H到点C的距离为10 cm,DF=20cm,EF∥AB,∠EHD=45°,求坐板EF的宽度.(本题答案均保留根号)
【答案】(1)35+![]() ;(2)坐板EF的宽度为(
;(2)坐板EF的宽度为(![]() )cm.
)cm.
【解析】
(1)如图,构造直角三角形Rt△AMC、Rt△CGD然后利用解直角三角形分段求解扶手前端D到地面的距离即可;
(2)由已知求出△EFH中∠EFH=60°,∠EHD=45°,然后由HQ+FQ=FH=20cm解三角形即可求解.
解:(1)如图2,过C作CM⊥AB,垂足为M,
又过D作DN⊥AB,垂足为N,过C作CG⊥DN,垂足为G,则∠DCG=60°,
∵AC=BC=60cm,AC、CD所在直线与地面的夹角分别为30°、60°,∴∠A=∠B=30°,
则在Rt△AMC中,CM=![]() =30cm.
=30cm.
∵在Rt△CGD中,sin∠DCG=![]() ,CD=50cm,
,CD=50cm,
∴DG=CDsin∠DCG=50sin60°=![]() =
=![]() ,
,
又GN=CM=30cm,前后车轮半径均为5cm,
∴扶手前端D到地面的距离为DG+GN+5=![]() +30+5=35+
+30+5=35+![]() (cm).
(cm).
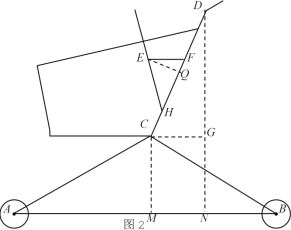
(2)∵EF∥CG∥AB,∴∠EFH=∠DCG=60°,
∵CD=50cm,椅子的支点H到点C的距离为10cm,DF=20cm,
∴FH=20cm,
如图2,过E作EQ⊥FH,垂足为Q,设FQ=x,
在Rt△EQF中,∠EFH=60°,∴EF=2FQ=2x,EQ=![]() ,
,
在Rt△EQH中,∠EHD=45°,∴HQ=EQ=![]() ,
,
∵HQ+FQ=FH=20cm,∴![]() +x=20,解得x=
+x=20,解得x=![]() ,
,
∴EF=2(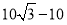 )=
)=![]() .
.
答:坐板EF的宽度为(![]() )cm.
)cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c的图象如图所示,以下结论:①b
+bx+c的图象如图所示,以下结论:①b![]() >4ac;②b+2a<0;③当x<-
>4ac;②b+2a<0;③当x<-![]() ,y随x的增大而增大;④a-b+c<0中,正确的有( )
,y随x的增大而增大;④a-b+c<0中,正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:
请解答下列问题:
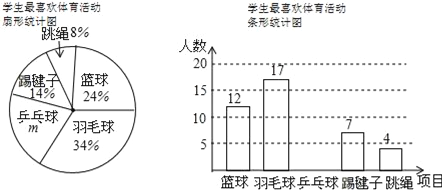
(1)m= %,这次共抽取了 名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
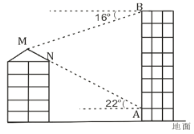
【题目】如图,小明在商城二楼地板![]() 处发现对五层居民楼顶防雨棚一侧斜面
处发现对五层居民楼顶防雨棚一侧斜面![]() 与点
与点![]() 在一条直线上,此时测得
在一条直线上,此时测得![]() ,
,![]() 仰角是
仰角是![]() ,上到九楼在地板边沿
,上到九楼在地板边沿![]() 点测得居民楼顶斜面顶端
点测得居民楼顶斜面顶端![]() 点俯角是
点俯角是![]() ,已知商城每层楼高
,已知商城每层楼高![]() 米,居民楼每层楼高
米,居民楼每层楼高![]() 米,试计算居民楼顶防雨棚一侧斜面
米,试计算居民楼顶防雨棚一侧斜面![]() 的长度.(结果保留精确到
的长度.(结果保留精确到![]() 米)(参考数据:
米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
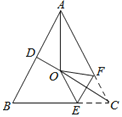
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有若辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》(分别用字母A、B、C依次表示这三部专著)等是我国古代数学的重要文献.将A、B、C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗均后放在桌面上小明先从中随机抽取张卡片,记录下卡片上的字母,放回后洗均,再由小强从中随机抽取张卡片,请用列表法或画树状图法,求小明和小强抽到的卡片上的字母相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
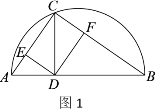
【题目】如图1,D是![]() 所对弦AB上一动点,过点D作CD⊥AB交
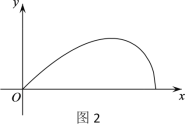
所对弦AB上一动点,过点D作CD⊥AB交![]() 于点C,连接AC,BC,过点D作AC,BC的垂线,分别交AC,BC于点E,F,设A,D两点间的距离为x,图1中某条线段的长为y(当线段的两个端点重合时,y的值为0),若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
于点C,连接AC,BC,过点D作AC,BC的垂线,分别交AC,BC于点E,F,设A,D两点间的距离为x,图1中某条线段的长为y(当线段的两个端点重合时,y的值为0),若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.线段CDB.线段BDC.线段DED.线段DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 与
与![]() 相交于点
相交于点![]() .
.
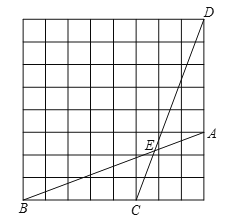
(1)![]() 的长等于 ;
的长等于 ;
(2)![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,在线段
,在线段![]() 上有一点
上有一点![]() ,满足
,满足![]() ,请在如图所示的网格中,用无刻度的直尺,画出点
,请在如图所示的网格中,用无刻度的直尺,画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明) .
的位置是如何找到的(不要求证明) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com