
����Ŀ���ھ���ABCD�У�AB=a��AD=b����MΪBC����һ���㣨��M���B��C���غϣ�������AM������M��MN��AM������ΪM��MN��CD��CD���ӳ����ڵ�N��
��1����֤����CMN�ס�BAM��
��2����BM=x��CN=y����y����x�ĺ�������ʽ����xȡ��ֵʱ��y�����ֵ�������y�����ֵ��
��3������M��BC���˶�ʱ����ʹ����������������������b��ȡֵ��Χ���ٵ�Nʼ�����߶�CD�ϣ��ڵ�M��ijһλ��ʱ����Nǡ�����D�غϣ�
���𰸡�
��1��
����𡿽⣺���ı���ABCD�Ǿ��Σ�
���B=��C=90�㣬
���BAM+��AMB=90�㣮
��MN��AM������AMN=90�㣬
���CMN+��AMB=90�㣬
���BAM=��CMN��
���CMN�ס�BAM��
��2��
�ߡ�CMN�ס�BAM��
��![]() ��
��
��BM=x��CN=y��AB=a��BC=AD=b��
��![]() ��
��
��y=![]() ��bx��x2��=
��bx��x2��=![]() ��x2��bx��
��x2��bx��
=![]() [��x��
[��x��![]() ��2��
��2��![]() ]
]
=![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
��![]() ��0��
��0��
�൱x=![]() ʱ��yȡ���ֵ�����ֵΪ
ʱ��yȡ���ֵ�����ֵΪ![]() ��
��
��3��
�����֪��
��0��x��bʱ��y�����ֵΪa����![]() =a��
=a��
��ã�b=2a��
��Ҫͬʱ��������������b��ֵΪ2a��
����������1�����ı���ABCD�Ǿ��οɵá�B=��C=90�㣬Ҫ֤��CMN�ס�BAM��ֻ��֤��BAM=��CMN���ɣ�
��2���������������ε����ʣ��ɡ�CMN�ס�BAM���ɵõ�y��x�ĺ�������ʽ��Ȼ��ֻ�������䷽���Ϳ����y�����ֵ��
��3���ɵ�M��BC���˶�����M���B��C���غϣ����ɵ�0��x��b��Ҫ���������٣�Ӧ��֤��0��x��bʱ��y��a�������Ҫ���������ڣ������һ��x��ʹ��y=a���ۺ������ٺ͢ڣ���0��x��bʱy���ֵӦΪa��Ȼ���ϣ�2���еĽ��ۣ��Ϳɽ�����⣮
�����㾫����������Ĺؼ�����������κ�������ֵ�����֪ʶ����������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a���Լ��Ծ��ε����ʵ����⣬�˽���ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ�


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶�Ʒ��ר�����������ס��������˶�Ь�����мס��������˶�Ь�Ľ��ۺ��ۼ����±�����֪����60˫�����˶�Ь��50˫�����˶�Ь����10000Ԫ
�˶�Ь�۸� | �� | �� |
���ۣ�Ԫ/˫�� | m | m��20 |
�ۼۣ�Ԫ/˫�� | 240 | 160 |
��1����m��ֵ��
��2��Ҫʹ�����ļס��������˶�Ь��200˫������������=�ۼ۩����ۣ�����21000Ԫ���Ҳ�����22000Ԫ���ʸ�ר�����м��ֽ���������
��3���ڣ�2���������£�ר�����������Լ����˶�Ьÿ˫�Ż�a��50��a��70��Ԫ���ۣ������˶�Ь�۸䣮��ô��ר����Ҫ����������Ӧ��ν�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����C��D�ǰ�Բ�����ȷֵ㣬�ӳ�AC��BD���ڵ�E�� 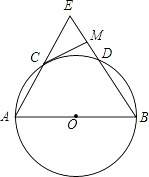
��1�����E�Ķ�����
��2����MΪBE��һ�㣬������EMEB=CE2 �� ����CM����֤��CMΪ��O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DΪAC�ߵ��е㣬��DB��BC��BC=4��CD=5��
��1����DB�ij���
��2���ڡ�ABC�У���BC���ϸߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1�����㣺������2��+��1+�У�0��|![]() |+
|+![]() ��
��
��2���Ȼ�������ֵ����x+2����x��2����x��x+3��������x=��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼڴ�����������ȫ��ͬ�Ŀ�Ƭ���ֱ���Щ�1��1��2���ҿڴ�������ȫ��ͬ�Ŀ�Ƭ���ֱ���Щ�2��3��4�����������ڴ��и����ȡ��һ�ſ�Ƭ��
��1������״ͼ���б���ʾ���п��ܳ��ֵĽ����
��2��������ȡ����Ƭ������֮��Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD����࣬���ȱ�������CDE������AE��BE�����AEB�Ķ���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��11�¶���ڣ�������Ϊͳ��ijѧУ����ѧ������״��������ͼ��
��1�����������ϵ�xֵ���μӵ����������������ȫͳ��ͼ��
��2���������ϵ�Բ�Ľ�Ϊ �� ��
��3��ȫ����6.7��ѧ�������������� �ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com