
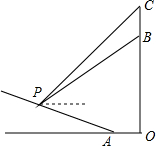
 如图,某高楼OB上有一旗杆CB,我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度,由于有其他建筑物遮挡视线不便测量,所以测量员沿坡度i=1:$\sqrt{3}$的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,某高楼OB上有一旗杆CB,我校数学兴趣小组的同学准备利用所学的三角函数知识估测该高楼的高度,由于有其他建筑物遮挡视线不便测量,所以测量员沿坡度i=1:$\sqrt{3}$的山坡从坡脚的A处前行50米到达P处,测得旗杆顶部C的仰角为45°,旗杆底部B的仰角为37°(测量员的身高忽略不计),已知旗杆高BC=15米,则该高楼OB的高度为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)| A. | 45 | B. | 60 | C. | 70 | D. | 85 |
分析 作PD⊥OC于D,PE⊥OA于E,根据坡度的概念求出∠PAE的度数,根据正弦的定义求出PE,根据正切的定义用PD表示出BD、CD,根据题意列出算式,求出PD,得到BD的长,根据OB=OD+BD计算即可.
解答 解:过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形,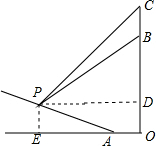
∴PE=OD,
∵AP坡的坡度i=1:$\sqrt{3}$,
∴tan∠PAE=$\frac{\sqrt{3}}{3}$,
∴∠PAE=30°,
∴PE=$\frac{1}{2}$AP=25,
在Rt△PBD中,∠BDP=90°,∠BPD=37°,
∴BD=PD•tan∠BPD≈$\frac{3}{4}$PD,
在Rt△CPD中,∠CDP=90°,∠CPD=45°,
∴CD=PD,
∵CD-BD=BC,
∴PD-$\frac{3}{4}$PD=15,
解得,PD=60,
∴BD=$\frac{3}{4}$×60=45,
∴OB=OD+BD=25+45=70,
故选:C.
点评 本题考查了解直角三角形的应用-仰角俯角问题、坡度坡角问题,正确作出辅助线,构造直角三角形,利用三角函数求解是解题的关键.


科目:初中数学 来源: 题型:解答题
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
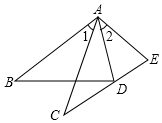 在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com