
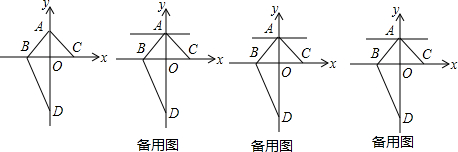
分析 (1)根据三角形面积公式求出AD即可.
(2)分两种情形①当0<t≤8时,②当t>8时,求出△PAC面积即可.
(3)分三种情形①如图1中,当∠QPR=90°,PQ=PR时,作RH⊥OP于H,②如图2中,当∠PQR=90°,QR=PQ时,③如图3中,当∠QRP=90°,QR=PR,利用全等三角形的性质列出方程即可解决.
解答 解:(1)∵A(0,6),B(-4,0),△ABD的面积是30,
∴$\frac{1}{2}$•AD•BO=30,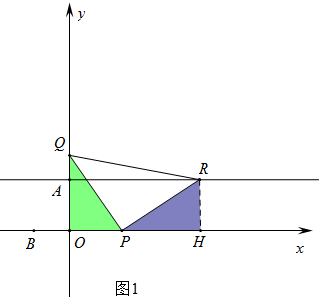
∴$\frac{1}{2}$•AD•4=30,
∴AD=15,
∴OD=9,
∴点D坐标为(0,-9).
(2)∵点B(-4,0)关于y轴的对称点为C点,
∴点C坐标(4,0),
∴当0<t≤8时,S=$\frac{1}{2}$×(8-t)×6=-3t+24,
当t>8时,S=$\frac{1}{2}$×(t-8)×6=3t-24.
(3)①如图1中,当∠QPR=90°,PQ=PR时,作RH⊥OP于H,
∵∠QPO+∠RPH=90°,∠QPO+∠PQO=90°,
∴∠PQO=∠RPH,
在△PQO和△RPH中,
$\left\{\begin{array}{l}{∠POQ=∠PHR=90°}\\{∠PQO=∠RPH}\\{PQ=PR}\end{array}\right.$,
∴△PQO≌RPH,
∴RH=PO,
∵四边形AOHR是矩形,
∴RH=AO=6,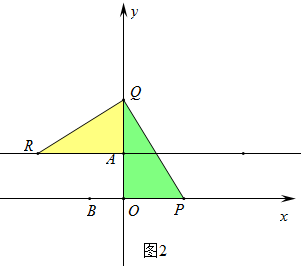
∴OP=6,
∴t-4=6,
∴t=10.
②如图2中,当∠PQR=90°,QR=PQ时,
∵∠RQA+∠OQP=90°,∠OQP+∠OPQ=90°,
∴∠RQA=∠OPQ,
在△ARQ和△OQP中,
$\left\{\begin{array}{l}{∠RAQ=∠POQ}\\{∠RQA=∠OPQ}\\{QR=PQ}\end{array}\right.$,
∴△ARQ≌△OQP,
∴OP=AQ,
∴t-4=2t-15,
∴t=11.
③ 如图3中,当∠QRP=90°,QR=PR,
如图3中,当∠QRP=90°,QR=PR,
∵∠RQA+∠PRH=90°,∠PRH+∠RPH=90°,
∴∠QRA=∠RPH,
在△AQR和△HRP中,
$\left\{\begin{array}{l}{∠QRA=∠RPH}\\{∠QAR=∠RHP}\\{QR=PR}\end{array}\right.$,
∴△AQR≌△HRP,
∴AQ=RH,AR=PH=AO=6,
∴OP=AH=RH-AR=AQ-AR=AQ-6
∴t-4=2t-15-6,
∴t=17.
综上所述t=10秒或11秒或17秒时,△PQR是等腰直角三角形.
点评 本题考查三角形综合题、等腰直角三角形的性质、全等三角形的判定和性质,解题的关键是正确画出图形,利用全等三角形性质解决问题,学会分类讨论,用方程的思想去思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
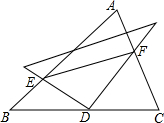 如图,点D是△ABC的边BC中点,将一把直角三角尺的直角顶点放于D处,其两条直角边分别交AB、AC于点E、F.试比较BE+CF与EF的大小,并说明理由.
如图,点D是△ABC的边BC中点,将一把直角三角尺的直角顶点放于D处,其两条直角边分别交AB、AC于点E、F.试比较BE+CF与EF的大小,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3+2x=1 | B. | 3(2-4x)-2x(4x-2)=1 | ||
| C. | 3(2-4x)+2x(4x-2)=4x-2 | D. | 3+2x=4x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com