
【题目】如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.

(1)当四边形EPQD为矩形时,求t的值.
(2)当以点E、P、C、Q为顶点的四边形是平行四边形时,求t的值;
(3)探索:是否存在这样的t值,使三角形PDQ是以PD为腰的等腰三角形?若存在,求出t的值,若不存在,请说明理由.
【答案】(1)t=![]() ;(2)t=1或t=3;(3)见解析
;(2)t=1或t=3;(3)见解析
【解析】
试题分析:(1)首先过点C作CF⊥AB于点F,可得AE=BF=3cm,由AB∥CD,∠DEF=90°,可得当EP=DQ时,四边形EPQD为矩形,即可得方程:2t﹣3=10﹣t,解此方程即可求得答案;
(2)由AB∥CD,可得当AP=CQ时,以点E、P、C、Q为顶点的四边形是平行四边形,然后分别从当P在AE左侧时与当P在AE右侧时去分析求解即可求得答案;
(3)首先由勾股定理表示出PD2,DQ2,PQ2,然后分别从PD=DQ或PD=PQ去分析求解即可求得答案.
解:(1)过点C作CF⊥AB于点F,
∵在等腰梯形ABCD中,AB∥DC,DE⊥AB,
∴DE=CF,
在Rt△ADE和Rt△BCF中,
![]() ,
,
∴Rt△ADE≌Rt△BCF(HL);
∴BF=AE,
∵AB=16cm,CD=10cm,
∴AE=BF=3cm,
根据题意得:AP=2tcm,CQ=tcm,
∴EP=AP﹣AE=2t﹣3(cm),DQ=CD﹣CQ=10﹣t(cm),
∵AB∥CD,∠DEF=90°,
∴当EP=DQ时,四边形EPQD为矩形,
∴2t﹣3=10﹣t,
解得:t=![]() ,
,
∴当四边形EPQD为矩形时,t=![]() ;
;
(2)∵AB∥CD,
∴当AP=CQ时,以点E、P、C、Q为顶点的四边形是平行四边形,
当P在AE左侧时,EP=AE﹣AP=3﹣2t(cm),
此时3﹣2t=t,解得:t=1,
当P在AE右侧时,EP=AP﹣AE=2t﹣3(cm),
此时2t﹣3=t,解得:t=3,
∴当以点E、P、C、Q为顶点的四边形是平行四边形时,t=1或t=3;
(3)存在.
理由:在Rt△ADE中,AE=3,AD=5,
∴DE=![]() =4,
=4,
∴PD2=PE2+DE2=(2t﹣3)2+42=4t2﹣12t+25,DQ2=(10﹣t)2=t2﹣20t+100,
过点Q作QM⊥AB于点M,则BM=BF+FM=3+t,
∴PM=AB﹣AP﹣BM=13﹣3t(cm),
∴PQ2=QM2+PM2=(13﹣3t)2+42=9t2﹣78t+185,
若PD=DQ,则4t2﹣12t+25=t2﹣20t+100,
解得:t=![]() (负值舍去);
(负值舍去);
若PD=PQ,则4t2﹣12t+25=9t2﹣78t+185,
解得:t1=![]() ,t2=10(舍去),
,t2=10(舍去),
综上可得:t=![]() 或t=
或t=![]() .
.



科目:初中数学 来源: 题型:
【题目】设p、q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此一次函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=![]() x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
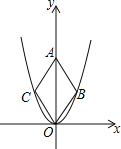
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
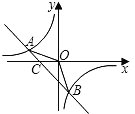
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求方程kx+b﹣![]() =0的解(请直接写出答案);
=0的解(请直接写出答案);
(4)求不等式kx+b﹣![]() <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:“如图,已知:四边形ABCD中,AD∥BC,∠D=67°,…”
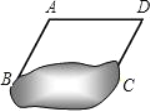
(1)根据以上信息,你可以求出∠A、∠B、∠C中的哪个角?写出求解的过程;
(2)若要求出其它的角,请你添上一个适当的条件: ,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A. 5x+4(x+2)=44 B. 5x+4(x﹣2)=44 C. 9(x+2)=44 D. 9(x+2)﹣4×2=44
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com