练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．某健身俱乐部有两种收费方式，甲方式为：缴纳50元会员费后，每次收费3元；乙方式为每次健身收费8元．
    （1）若小王去健身x次，按甲、乙两种方式各应缴费多少元？
    （2）若小王去健身12次，你认为他采用哪种方式合算？

    分析 （1）根据题意列出代数式解答即可；
    （2）把x=12代入代数式解答即可．

    解答 解：（1）按甲种方式应缴费为50+3x；
    按乙种方式应缴费为8x；
    （2）把x=12代入50+3x=86元；
    把x=12代入x=96元，
    所以他采用甲种方式合算．

    点评 本题主要考查列代数式，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的数量关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．已知abc＞0，求$\frac{ab}{|ab|}$+$\frac{ac}{|ac|}$+$\frac{bc}{|bc|}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．将下列各式分解因式：
    （1）因式分解：（x2+4）2-16x2．
    （2）解不等式组：$\left\{\begin{array}{l}{x+2≥-1}\\{3x-1＜5}\end{array}\right.$，并将解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．汽车刹车后行驶的距离s（单位：m）关于行驶的时间t（单位：s）的函数解析式是s=15t-6t2．汽车刹车后到停下来前进了多远？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先阅读，后解答：
    $\frac{\sqrt{3}}{\sqrt{3}-\sqrt{2}}$=$\frac{\sqrt{3}（\sqrt{3}+\sqrt{2}）}{（\sqrt{3}-\sqrt{2}）（\sqrt{3}+\sqrt{2}）}$=$\frac{3+\sqrt{6}}{3-2}$=3+$\sqrt{6}$
    像上述解题过程中，$\sqrt{3}$-$\sqrt{2}$与$\sqrt{3}$+$\sqrt{2}$相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化，
    （1）$\sqrt{3}$的有理化因式是$\sqrt{3}$； $\sqrt{5}$+2的有理化因式是$\sqrt{5}$-2．
    （2）将下列式子进行分母有理化：
    $\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$；$\frac{1}{3+\sqrt{6}}$=1-$\frac{\sqrt{6}}{3}$．
    （3）已知a=$\frac{1}{2+\sqrt{3}}$，b=2-$\sqrt{3}$，比较a与b的大小关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图所示，P为正方形ABCD的边AD上的一个动点，AE⊥BP，CF⊥BP，垂足分别为点E、F，已知AD=4．
    （1）证明：△ABE≌△BCF；
    （2）过点P作PM∥FC交CD于点M，点P在何位置时线段DM最长，并求出此时DM的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，把直角三角板的直角顶点O放在破损玻璃镜的圆周上，两直角边与圆弧分别交于点M、N，量得OM=8cm，ON=6cm，则该圆玻璃镜的半径是5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

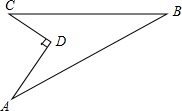    7．如图，某住宅小区在施工过程中留下了一块空地，已知AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米300元，试问用该草坪铺满这块空地共需花费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

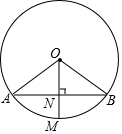    8．如图，在⊙O中，半径OM垂直弦AB于点N．
    （1）若AB=2$\sqrt{3}$，ON=1，求MN的长；
    （2）若AB=2$\sqrt{3}$，MN=1，求ON的长．

    查看答案和解析>>

    同步练习册答案