
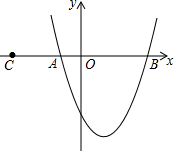
 如图,已知二次函数y=(x+1)(x-3)交x轴于A、B两点,直线l过点C(-3,0).
如图,已知二次函数y=(x+1)(x-3)交x轴于A、B两点,直线l过点C(-3,0).分析 (1)过AB的中点E作⊙E,若直线l与⊙E相切时,此时切点即为D,这时直线l上只有一个点能使∠ADB=90°,利用勾股定理即可求出D的坐标,由于圆具有对称性,所以直线l有两种情况;
(2)⊙M与抛物线相交于点E,设点E的坐标为(m,m2-2m-3),利用相似三角形的性质即可求出点E的坐标.
解答 解:(1)过AB的中点M作⊙M,
过点C作直线l与⊙O相切,切点为D,
令y=0代入y=(x+1)(x-3),
∴x=-1或x=3,
∴A(-1,0),B(3,0),
∴点M(1,0),AB=4,
过点D作DO′⊥x轴,
∵CM=4,DM=$\frac{1}{2}$AB=2,
∴sin∠DCM=$\frac{DM}{CM}$=$\frac{1}{2}$,
∴tan∠DCM=$\frac{\sqrt{3}}{3}$,∠DCM=30°,
∴由勾股定理可求得:CD=2$\sqrt{3}$,
∴DO′=$\frac{1}{2}$CD=$\sqrt{3}$
∴$\frac{DO′}{CO′}$=$\frac{\sqrt{3}}{3}$,
∴CO′=3,
即O′与O重合,
∴D(0,$\sqrt{3}$),
设直线l的解析式为y=kx+b,
把(0,$\sqrt{3}$)和(-3,0)代入y=kx+b,
∴解得:$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\sqrt{3}}\end{array}\right.$,
∴直线l的解析式为:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
由于圆具有对称性,所以点D的坐标也可以是(0,-$\sqrt{3}$),
同理可求得的直线l的解析式为:y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$;
综上所述,直线l的解析式为y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$或y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$;
(2)设⊙M与抛物线交于点E,
过点E作EF⊥x轴于点F,
∴由圆周角定理可知:∠AEB=90°,
∵∠AEF+∠FAE=∠FAE+∠ABE=90°,
∴∠AEF=∠ABE,
∴△AEF∽△ABE,
∴EF2=AF•BF,
设E(m,m2-2m-3),
∴EF=-(m2-2m-3),AF=m+1,BF=3-m,
∴[(m+1)(m-3)]2=(m+1)(3-m),
∴(m+1)(m-3)=-1,
∴m=1±$\sqrt{2}$,
∴E(1±$\sqrt{2}$,-1),
点评 本题考查二次函数综合问题,涉及圆周角定理,相似三角形的判定,勾股定理等知识,综合程度较高.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | ①③④ | B. | ①②④ | C. | ③④② | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x3•3x4=6x12 | B. | 4a2•3a3=12a5 | C. | 3m3•5m3=15m3 | D. | 4y•(2y3)2=8y7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.
如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2与-3 | B. | -3与-$\frac{1}{3}$ | C. | 2 014与-2 013 | D. | -0.25与$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,∠BAC=90°,点D,E,F分别在边BC、AB、AC上,BD=DC,BE=AF,EF交AD于点G.请在图中找一下,与△BDE相似的三角形有哪些?
如图,在△ABC中,AB=AC,∠BAC=90°,点D,E,F分别在边BC、AB、AC上,BD=DC,BE=AF,EF交AD于点G.请在图中找一下,与△BDE相似的三角形有哪些?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在《实践与探究》活动中,小亮和小红分别用8个一样大小的长方形纸片拼图,小亮恰好拼成一个大的长方形,如图1所示,小红拼成如图2所示的正方形,但中间还留下一个边长为3cm的小正方形,请你通过计算,算出每个小长方形的面积是135cm2.
在《实践与探究》活动中,小亮和小红分别用8个一样大小的长方形纸片拼图,小亮恰好拼成一个大的长方形,如图1所示,小红拼成如图2所示的正方形,但中间还留下一个边长为3cm的小正方形,请你通过计算,算出每个小长方形的面积是135cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com