
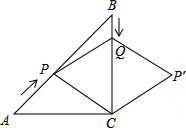
 如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒| 2 |
| 2 |
| ||
| 2 |
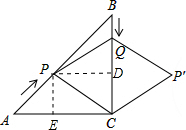 解:作PD⊥BC于D,PE⊥AC于E,如图,AP=
解:作PD⊥BC于D,PE⊥AC于E,如图,AP=| 2 |
| ||
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
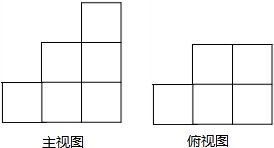 如图,是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的个数为n,则n不可能是( )
如图,是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的个数为n,则n不可能是( )| A、9 | B、10 | C、11 | D、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
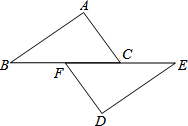 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.供选择的三个条件(请从其中选择一个):①∠A=∠D;②BC=EF;③AB=ED.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.供选择的三个条件(请从其中选择一个):①∠A=∠D;②BC=EF;③AB=ED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com