
【题目】如图,在Rt△ABC中,∠BCA=90°,∠DCA=30°,AC=![]() ,AD=
,AD=![]() ,则BC的长为__.
,则BC的长为__.

科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
的图象的一支位于第一象限,点A(x1,y1),B(x2,y2)都在该函数的图象上.
(1)m的取值范围是 ,函数图象的另一支位于第一象限,若x1>x2,y1>y2,则点B在第 象限;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点C与点A关于x轴对称,若△OAC的面积为6,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动,试解决下列问题:
(1)求直线AC的解析式;
(2)求△OAC的面积;
(3)是否存在点M、使△OMC的面积是△OAC的面积的![]() ?若存在,求出此时点M的坐标;若不存在,请说明理由?
?若存在,求出此时点M的坐标;若不存在,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AC=BC=4,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由;
(2)点P在滑动时,当AP长为多少时,△ADP与△BPC全等,为什么?
(3)点P在滑动时,△PCD的形状可以是等腰三角形吗?若可以,请求出夹角α的大小;若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只口袋里放着![]() 个红球、
个红球、![]() 个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.
![]() 取出红球的概率为
取出红球的概率为![]() ,白球有多少个?
,白球有多少个?
![]() 取出黑球的概率是多少?
取出黑球的概率是多少?
![]() 再在原来的袋中放进多少个红球,能使取出红球的概率达到
再在原来的袋中放进多少个红球,能使取出红球的概率达到![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
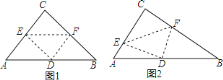
【题目】在![]() 中,
中,![]() ,翻折
,翻折![]() ,使点
,使点![]() 落在斜边
落在斜边![]() 上某一点
上某一点![]() 处,折痕为
处,折痕为![]() (点
(点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上)
上)
![]() 当
当![]() 时,若
时,若![]() 与
与![]() 相似(如图
相似(如图![]() ),求
),求![]() 的长;
的长;
![]() 当点
当点![]() 是
是![]() 的中点时(如图
的中点时(如图![]() ),
),![]() 与
与![]() 相似吗?请说明理由.
相似吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com