
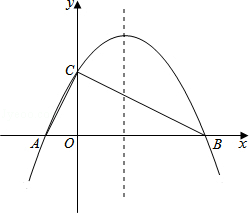
 ��ͼ����֪������y=-$\frac{1}{4}$x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C��0��4��������֪A�������ΪA��-2��0����
��ͼ����֪������y=-$\frac{1}{4}$x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C��0��4��������֪A�������ΪA��-2��0�������� ��1������C�����꣬�ɵ�c��ֵ������A�����꣬�ɵ�b��ֵ��
��2���������εĶԳ��ᴹֱ�һ���ƽ�֣��ɵ�P�ĺ����꣬���������߽���ʽ�õ����ꣻ
��3������������ֱ�������ü��ɣ�
��4���ֱ�ӡ�QCB=90�㣬��QBC=90�㣬��CQB=90��������ȥ���������ݹ��ɶ����������ڷ�����⼴����ô𰸣�
��� �⣺��1����������y=-$\frac{1}{4}$x2+bx+c��y���ཻ�ڵ�C��0��4����
��c=4��
��y=-$\frac{1}{4}$x2+bx+4��
��������y=-$\frac{1}{4}$x2+bx+4��x���ཻ��A��B���㣬A��-2��0����
��-$\frac{1}{4}$��4-2b+4=0��
���b=$\frac{3}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��2����y=0����0=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
���x1=-2��x2=8��
��B��8��0����
���ı���BPOH����OBΪ�Խ��ߵ����Σ��������ε����ʣ���P����ֱ��x=4�ϣ�
�֡ߵ�P��������y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4�ϣ�
��y=-$\frac{1}{4}$��16+$\frac{3}{2}$��4+4=6��
��P��4��6����
�����������ϴ��ڵ�P��4��6����ʹ���ı���BPOH�����Σ�
��3����M��ֱ��BC�Ϸ�ʱ��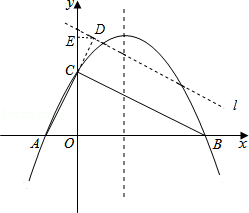
��A��-2��0����B��8��0����C��0��4����
��AB=10��OC=4��BC=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$��
��S��ABC=$\frac{1}{2}$��10��4=20��
�ߡ�BCM��������ABC�������ȣ�
��$\frac{1}{2}$BC•h=20��
��h=$\frac{40}{4\sqrt{5}}$=2$\sqrt{5}$��
��CD��BC��ʹCD=4$\sqrt{5}$����D����DE��y����E�����CDE�ס�CBO��
��$\frac{CE}{OB}$=$\frac{DE}{OC}$=$\frac{CD}{BC}$����$\frac{CE}{8}$=$\frac{DE}{4}$=$\frac{2\sqrt{5}}{4\sqrt{5}}$��
��CE=4��DE=2��
��D��2��8����
��B��8��0����C��0��4����
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+4��
��D����ֱ��l��BC����ֱ��l�Ľ���ʽΪy=-$\frac{1}{2}$x+b��
����D��2��8����8=-$\frac{1}{2}$��2+b��
���b=9��
��ֱ��lΪy=-$\frac{1}{2}$x+9��
��-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{2}x$+9��
������x2-8x+20=0��
�ߡ�=64-4��20��0��
����ֱ��BC���Ƿ�������������M�㣬
��M��ֱ��BC�·�ʱ��
��A����BC��ƽ����l����ֱ��l�Ľ���ʽΪy=-$\frac{1}{2}$x+b��
����A��-2��0����0=-$\frac{1}{2}$��2+b��
���b=-1��
��y=-$\frac{1}{2}$x-1��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x-1}\\{y=-\frac{1}{4}{x}^{2}+\frac{3}{2}x+4}\end{array}\right.$��$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=10}\\{y=-6}\end{array}\right.$��
��M��10��-6����
���ϣ����������ϴ��ڵ�M��ʹ��BCM��������ABC�������ȣ���M������Ϊ��10��-6����
��4���������ߵĶԳ���Ϊ��ֱ��x=-$\frac{\frac{3}{2}}{2����-\frac{1}{4}��}$=3��
������ڵ�Q��ʹ��BCQΪֱ��������
����Q��3��m����
��B��8��0����C��0��4����B
��BC2=80��BQ2=��8-3��2+m2=25+m2��CQ2=9+��4-m��2��
����QCB=90��ʱ����QC2+BC2=QB2��
��9+��4-m��2+80=25+m2��
���m=10��
��Q��3��10����
����QBC=90ʱ����QB2+BC2=QC2��
��9+��4-m��2=80+25+m2��
���m=-10��
��Q��3��-10����
����BQC=90��ʱ����QB2+QC2=BC2��
��9+��4-m��2+25+m2=80��
���m=2��$\sqrt{19}$��
��Q��3��2+$\sqrt{19}$����Q��3��2-$\sqrt{19}$����
�����������Q������ΪQ1��3��10����Q2��3��-10����Q3��3��2+$\sqrt{19}$����Q4��3��2-$\sqrt{19}$����
���� ���⿼���˴���ϵ��������κ����Ľ���ʽ�������ε����ʣ�ֱ�������ε��ж��Լ������ε������֪ʶ�������Ѷ����У�ע���������˼�룬����˼�������ν��˼���Ӧ���ǽ����Ĺؼ���


 Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
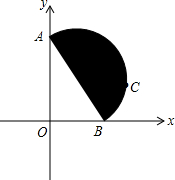 ��ͼ����ABΪֱ���İ�Բ����Ƭ����ͼ��ʾ��λ��ƽ��б�����������ϣ���C�ǰ�ԲƬ��AB�Ͽ���B���һ�����㣬�ֵ�A����y�����յ�O������ͬʱ��B��Ӧ������x�������������жϣ��ڻ��������У���C���O����ı仯����ǣ�������
��ͼ����ABΪֱ���İ�Բ����Ƭ����ͼ��ʾ��λ��ƽ��б�����������ϣ���C�ǰ�ԲƬ��AB�Ͽ���B���һ�����㣬�ֵ�A����y�����յ�O������ͬʱ��B��Ӧ������x�������������жϣ��ڻ��������У���C���O����ı仯����ǣ�������| A�� | һֱ���� | B�� | ���ֲ��� | C�� | �ȼ�С������ | D�� | ��������С |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=ax2+c��a��0����y�ύ�ڵ�A����x�ύ�ڵ�B��C���㣨��C��x���������ϣ�����ABCΪ����ֱ�������Σ������Ϊ4���ֽ���������BA����ƽ�ƣ�ƽ�ƺ�������߾�����Cʱ����x�����һ����ΪE���䶥��ΪF���Գ�����x��Ľ���ΪH���ֽ�һ�㹻������ǰ��ֱ�Ƕ���Q��������AF������HF�ϣ�һֱ�DZ�ʼ�չ���E����һֱ�DZ���y���ཻ�ڵ�P�������������ĵ�Q��ʹ�Ե�P��Q��EΪ��������������POEȫ�ȣ����Q������Ϊ��6��2$\sqrt{21}$����6��3����10��12����4+$\sqrt{14}$��6+$\sqrt{14}$����4-$\sqrt{14}$��6-$\sqrt{14}$����
��ͼ��������y=ax2+c��a��0����y�ύ�ڵ�A����x�ύ�ڵ�B��C���㣨��C��x���������ϣ�����ABCΪ����ֱ�������Σ������Ϊ4���ֽ���������BA����ƽ�ƣ�ƽ�ƺ�������߾�����Cʱ����x�����һ����ΪE���䶥��ΪF���Գ�����x��Ľ���ΪH���ֽ�һ�㹻������ǰ��ֱ�Ƕ���Q��������AF������HF�ϣ�һֱ�DZ�ʼ�չ���E����һֱ�DZ���y���ཻ�ڵ�P�������������ĵ�Q��ʹ�Ե�P��Q��EΪ��������������POEȫ�ȣ����Q������Ϊ��6��2$\sqrt{21}$����6��3����10��12����4+$\sqrt{14}$��6+$\sqrt{14}$����4-$\sqrt{14}$��6-$\sqrt{14}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABO�ա�BA��B�䣬A��0��2����B��-1��0����
��ͼ����ABO�ա�BA��B�䣬A��0��2����B��-1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com