
(本题满分10分)
已知:如图,在Rt△ABC中,∠ACB=90º,AC=6,sinB=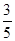 , 点D是边BC的中点,
, 点D是边BC的中点,
CE⊥AD,垂足为E.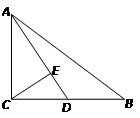
求:(1)线段CD的长;
(2)cos∠DCE的值.
(1)4
(2)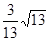
解析考点:解直角三角形.
分析:(1)在直角△ABC中,根据∠B的正弦即可求得AC,根据勾股定理即可求得BC,进而得到CD的长;
(2)∠DCE=∠CAD,只要在直角△ACD中求出∠CAD的余弦值即可.
解答:解:(1)在Rt△ABC中,∵∠C=90°,AC=6,sinB=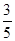 ,
,
∴AB=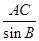 =6×
=6× =10.
=10.
BC=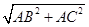 =
=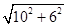 =8.
=8.
CD=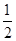 BC=4;
BC=4;
(2)在Rt△ACD中,∵CE⊥AD,
∴∠CAD=90°-∠ACE=∠DCE.(6分)
AD=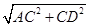 =
= =2
=2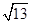 .
.
∴cos∠DCE=cos∠CAD=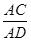 =
=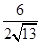 =
=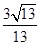 .
.
点评:在锐角的三角函数中,已知其中的一个就可求出另外几个,并且三角函数值的大小只与角的大小有关,而与所在三角形无关.


科目:初中数学 来源: 题型:

 图象与x轴交点坐标;
图象与x轴交点坐标;查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(江苏扬州卷)数学 题型:解答题
(本题满分10分)已知:如图,锐角 的两条高
的两条高 相交于点
相交于点 ,且
,且
(1)求证: 是等腰三角形;
是等腰三角形;
(2)判断点 是否在
是否在 的角平分线上,并说明理由.
的角平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省常州市考模拟联考数学卷 题型:解答题
(本题满分10分)已知:甲、乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到B地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.

1.(1)求甲车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
2.(2)当它们行驶到与各自出发地的距离相等时,用了 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围;
3.(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)
已知:如图,在Rt△ABC中,∠ACB=90º,AC=6,sinB=![]() ,点D是边BC的中点,
,点D是边BC的中点,
CE⊥AD,垂足为E.

求:(1)线段CD的长;
(2)cos∠DCE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com