
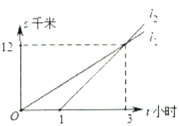
【题目】如图,![]() 两地相距
两地相距![]() 千米,甲、乙两人都从
千米,甲、乙两人都从![]() 地去
地去![]() 地,图中
地,图中![]() 和
和![]() 分别表示甲、乙两人所走路程
分别表示甲、乙两人所走路程![]() (千米)与时间
(千米)与时间![]() (小时)之间的关系,下列说法: ①乙晚出发
(小时)之间的关系,下列说法: ①乙晚出发![]() 小时;②乙出发
小时;②乙出发![]() 小时后追上甲;③甲的速度是
小时后追上甲;③甲的速度是![]() 千米/小时; ④乙先到达
千米/小时; ④乙先到达![]() 地.其中正确的是__________.(填序号)
地.其中正确的是__________.(填序号)
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )

A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形的判定
(1)有一个角是________________的三角形是直角三角形.
(2)有两个角________________的三角形是直角三角形.
(3)勾股定理的逆定理:如果三角形两边的平方和等于________________,那么这个三角形是直角三角形.
(4)如果三角形一边上的________________等于这边的一半,那么这个三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
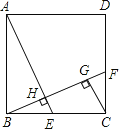
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() .
.
(1)点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,边
,边![]() 与
与![]() 轴交于点
轴交于点![]() .
.
①如图1,当点![]() 刚好落在
刚好落在![]() 轴上时,求点
轴上时,求点![]() 的坐标
的坐标
②如图2,当![]() 时,若线段
时,若线段![]() 在
在![]() 轴上移动得到线段
轴上移动得到线段![]() (线段
(线段![]() 平移时
平移时![]() 不动),当△A′O′Q′周长最小时,求OO′的长度.
不动),当△A′O′Q′周长最小时,求OO′的长度.
(2)如图3,若点![]() 为边
为边![]() 上一点(点
上一点(点![]() 不与
不与![]()
![]() 重合),沿
重合),沿![]() 将纸片折叠得
将纸片折叠得![]() 的对应点
的对应点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
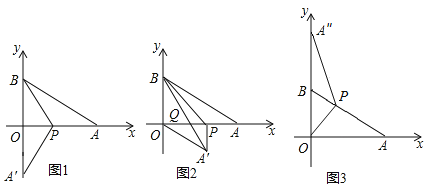
查看答案和解析>>
科目:初中数学 来源: 题型:
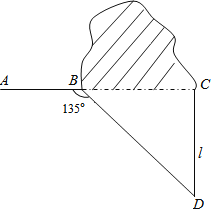
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
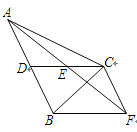
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,AB=8,点E是射线DC上一个动点(点E与点D不重合),连接AE,BE,以BE为边在线段AD的右侧作正方形BEFG,连结CG.
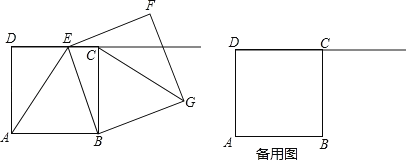
(1)当点E在线段DC上时,求证:△BAE≌△BCG;
(2)在(1)的条件下,若CE=2,求CG的长;
(3)连接CF,当△CFG为等腰三角形时,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com