
【题目】露露家里新购进了一台电热水器,她对电热水器的工作原理充满好奇.查阅说明书得知,电热水器上面显示的温度为内部水箱中水的温度,每次加热前可以预设温度值,当电热水器达到预设温度后,电热水器将停止加热,开启保温功能.而在使用过程中,电热水器会自动加水,水温会下降.
露露发现电热水器中水箱的温度y(单位:℃)与接通电源后的时间x(单位:min)之间存在函数关系,她打开电热水器的开关,预设温度为70℃,并记录水温变化的情况见下表,其中在接通电源后的第8min时,电热水器达到预设温度;第18min时,妈妈开始使用电热水器.
时间x(单位:min) | 0 | 2 | 4 | 6 | 8 | 18 | 20 | 21 | 25 | 28 |
温度y(单位:℃) | 30 | 40 | 50 | 60 | 70 | 70 | 63 | m | 50.4 | 45 |
(1)m的值为_________;
(2)请在下面的坐标系中描出上表中所有数据对应的点,并根据描出的点,画出当![]() 时,温度y随时间x变化的函数图象;
时,温度y随时间x变化的函数图象;

(3)在露露的妈妈使用电热水器前,电热水器处于保温功能的时长为__________min;
(4)未加热前,电热水器的水箱中水的温度为_________℃.
【答案】(1)60;(2)详见解析;(3)10;(4)30
【解析】
(1)根据x与y的关系,根据图表,第21分钟水的温度应该在63到50.4之间;
(2)根据表格中的数据将每个点在坐标中标出来再用平滑的曲线连接即可;
(3)根据表格第8分钟的时候已经到达设置温度,在第18分钟时才是用,这段时间均处于保温状态;
(4)根据表格中的数据,在0分钟时,温度为30
(1)根据表格中的数据对比即可得到m应该在60左右均可以
(2)根据表格中的数据将每个点在坐标中标出来再用平滑的曲线连接得到如下图形:
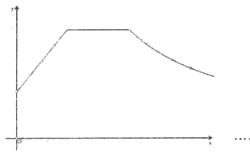
(3)根据表格第8分钟的时候已经到达设置温度,在第18分钟时才是用,这段时间均处于保温状态,故保温时间为18-8=10
(4)根据表格中的数据,在0分钟时,温度为30,因此水箱中的水为30


科目:初中数学 来源: 题型:
【题目】甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,根据图像信息,以上说法正确的是( )
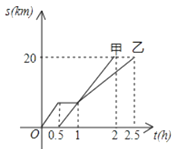
A.甲和乙两人同时到达目的地;B.甲在途中停留了0.5h;
C.相遇后,甲的速度小于乙的速度;D.他们都骑了20km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2,再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3,…,依次进行下去,则点B6的坐标是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形![]() ,请你通过计算说明点
,请你通过计算说明点![]() 在双曲线上.
在双曲线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连结BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC其中结论正确的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(-4,0),B(6,0),C(2,4),D(-3,2).
(1)求四边形ABCD的面积;
(2)在y轴上找一点P,使△APB的面积等于四边形的一半,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
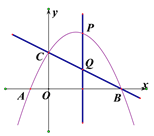
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+2的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=
x+2的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=![]() 对称,且经过A. C两点,与x轴交于另一点为B.
对称,且经过A. C两点,与x轴交于另一点为B.
(1)求抛物线的解析式;
(2)若点P为直线AC上方的抛物线上的一点,过点P作PQ⊥x轴于M,交AC于Q,求PQ的⊥最大值,并求此时△APC的面积;
(3)在抛物线的对称轴上找出使△ADC为直角三角形的点D,直接写出点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com