
【题目】以直线x=1为对称轴的抛物线y=-x2+bx+c与x轴交于A、B两点,其中点A的坐标为(3,0).
(1)求点B的坐标;
(2)设点M(x1,y1)、N(x2,y2)在抛物线线上,且x1<x2<1,试比较y1、y2的大小.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
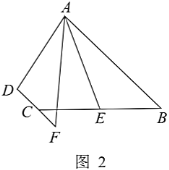
【题目】在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点
的中点
情景引入:
(1)如图1,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,DC之间的等量关系.
,DC之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断
转化在一个三角形中即可判断![]() ,
,![]() ,
,![]() 之间的等量关系为
之间的等量关系为![]() ,试证明该结论;
,试证明该结论;

问题探究:
(2)如图2,点![]() 是
是![]() 的延长线上一点,连
的延长线上一点,连![]() ,若
,若![]() 恰好是
恰好是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
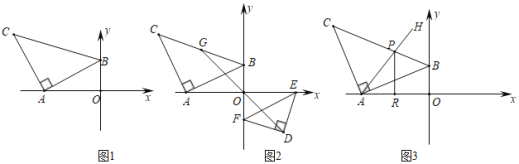
【题目】如图1,将任意一个等腰直角三角板△ABC放至平面直角坐标系xOy中,直角顶点A(a,0)在x轴的负半轴,点B(0,b)在y轴的正半轴,点C落在第二象限,
(1)若![]() =﹣b2+4b﹣4,求C点坐标;
=﹣b2+4b﹣4,求C点坐标;
(2)如图2,再将任意的一个等腰直角三角板△DEF放至平面直角坐标系xOy中,点E在x轴的正半轴上,F在y轴的负半轴上,直角顶点D落在第四象限,设点G为BC的中点,证明:点D,O,G三点刚好在同一条直线上;
(3)已知a=﹣4,b<4.如图3,点O关于直线AB的对称点为点H,AH交线段BC于点P,PR⊥x轴于点R,求△APR的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
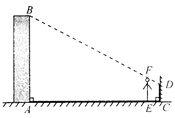
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°.
(1)尺规作图作出AB的垂直平分线DE,分别与AC、AB交于点D、E.并连结BD;(保留作图痕迹,不写作法)

(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com