
����Ŀ��Ϊ��Ӧ��ѧ�桢���·硢��������ѧ�����ĺ��٣�ijУ��չ��־Ը�߷��������Ŀ�С�����������������������ͨ�ڡ������ذ����ˡ���������ֲ���������������������ڼ䣬�����ȡ�˲���ѧ����־˼�߷���������е��飬������֣��������ÿ��ѧ���������˻�����ٵIJ�����1����IJ�����5����ݵ��������������²�����������ͳ��ͼ������ͳ��ͼ��
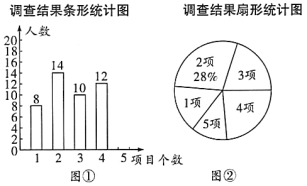
��������ͳ��ͼ����������⣺
��1�����������ȡ��ѧ������______����
��2����ȫ����ͳ��ͼ��
��3������У��3000��ѧ��������Ʋ�����4����ѧ��������
��4�����������ѧ�������ѡȡһ��̸��ĵã���ѡ�в�����5����ѧ���ĸ��ʣ�
���𰸡���1��50����2����ȫ����ͳ��ͼ����������3�����Ʋ�����4����ѧ����Լ��720�ˣ���4��![]() ��ѡ�в�����5����ѧ����
��ѡ�в�����5����ѧ����![]() ��
��
��������
��1�����ݲ���2�������Ϊ14����ռ�������������28%�����г������㼴�ɵó���ȡѧ������������
��2����������ȥ�μӻ��Ŀ�����ֱ�Ϊ1�2�3�4������������ɵó�����5�������������ɲ�ȫ����ͳ��ͼ��
��3��������ѧ���������Բ�����4����ѧ����ռ�İٷֱȣ����ɵó��𰸣�
��4�����ø��ʹ�ʽ��⼴�ɣ�
�⣺��1�����������ȡ��ѧ�����У�
![]() ������
������
�𣺱������ȡ��ѧ����50����
��2�����Ϊ5�������Ϊ��![]() ����
����
��ȫ����ͳ��ͼ���ͼ��

��3��![]() ���ˣ�.
���ˣ�.
����Ʋ�����4����ѧ����Լ��720�ˣ�
��4���߹���ȡ��50��ѧ�������в�����5����ѧ����6����
��![]() ��ѡ�в�����5����ѧ����
��ѡ�в�����5����ѧ����![]() .
.


 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0����4a+2b+c��0����![]() ��a��
��a��![]() ����b��c�����к�������ȷ���۵�ѡ���ǣ� ��
����b��c�����к�������ȷ���۵�ѡ���ǣ� ��

A.�٢ڢ�B.�٢ۢ�C.�ڢۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������۸��߸ߣ������������������ĸ߶ȹ�ע�����г������ƽ���۸�ÿǧ�˴ﵽһ���ĵ���ʱ��������Ͷ�봢��������ƽ������۸�
��1����ȥ�����������3��20�գ�����۸��߸ߣ�3��20�ձ�ȥ����۸�������60%��ij�����ڽ���3��20�չ���2.5ǧ����������Ҫ��200ԪǮ����ôȥ������������ͼ۸�Ϊÿǧ�˶���Ԫ��
��2��3��20�գ�����۸�Ϊÿǧ��60Ԫ��3��21�գ�ij�о���Ͷ�봢�����Ⲣ�涨�����ۼ���ÿǧ��60Ԫ�Ļ������µ�a%���ۣ�ij���а��涨�۳���һ���������⣬�ó����ڷǴ�������ļ۸���Ϊÿǧ��60Ԫ������£����������������������3��20��������a%���Ҵ������������ռ��������![]() �������������۵��ܽ���3��20�������
�������������۵��ܽ���3��20�������![]() ����a��ֵ��
����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019����߽���������˶��ᣨ7thCISMMilitaryWorldGames����2019��10��18����27�����й��人���У������й���һ�γа��ۺ��Թ��ʾ������£�Ҳ�Ǽ̱������˻���й��ٰ�Ĺ�ģ���Ĺ�������ʢ�ᣮij����˶�Ա��һ��ѵ���������10�Σ��ɼ���ͼ��ʾ�����н����в���ȷ���У���������
��������8������λ����8����ƽ������8���ܷ�����1.6��
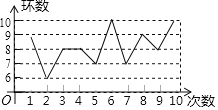
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������Ʒ�Ƶ�![]() ��ƹ���۸���7��8��9����λ��Ԫ�����֣���������ó�һ������֪
��ƹ���۸���7��8��9����λ��Ԫ�����֣���������ó�һ������֪![]() ��һ���õ�
��һ���õ�![]() Ԫ��
Ԫ��![]() ��
��
��1������![]() ����۸��������
����۸��������
��2��������������һ��![]() Ԫ��ѵ������������ʣ��
Ԫ��ѵ������������ʣ��![]() �����������һ��ѵ����
�����������һ��ѵ����
����ʣ��![]() ����۸����λ����ԭ��
����۸����λ����ԭ��![]() ����۸����λ���Ƿ���ͬ������Ҫ˵�����ɣ�
����۸����λ���Ƿ���ͬ������Ҫ˵�����ɣ�
������������ó�һ�����Żأ�֮���������һ�������б�������ͼ�����������ζ��õ�8Ԫ��ĸ��ʣ�
���� ���� | |||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
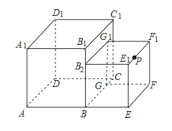
����Ŀ���ⳤ�ֱ�Ϊ![]() ��������������ͼ���ã���
��������������ͼ���ã���![]() ��
��![]() ��
��![]() ��ͬһֱ���ϣ�����
��ͬһֱ���ϣ�����![]() �����ϣ���
�����ϣ���![]() ��
��![]() ���е㣮һֻ����Ҫ����������ı���ӵ�
���е㣮һֻ����Ҫ����������ı���ӵ�![]() ������
������![]() �������е���̾�����__________��
�������е���̾�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
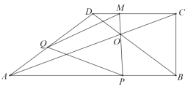
����Ŀ����֪����ͼ���ı���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �������˶����˶��ٶ�Ϊ
�������˶����˶��ٶ�Ϊ![]() ������
������![]() �ӵ�
�ӵ�![]() ��ʼ��
��ʼ��![]() �������˶����˶��ٶ�Ϊ
�������˶����˶��ٶ�Ϊ![]() ����
����![]() �͵�
�͵�![]() ͬʱ������
ͬʱ������![]() Ϊ�ı���
Ϊ�ı���![]() �ĶԽ��ߵĽ��㣬����
�ĶԽ��ߵĽ��㣬����![]() ���ӳ���
���ӳ���![]() ��
��![]() ������
������![]() �����˶���ʱ��Ϊ
�����˶���ʱ��Ϊ![]() ��
��![]() ��
��
��1����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
��2���������![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3�����˶������У��Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() ��������������
��������������![]() �����
�����![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��4�����˶������У��Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() ��
��![]() �Ĵ�ֱƽ�����ϣ������ڣ����
�Ĵ�ֱƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
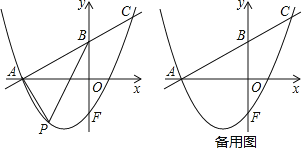
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�ֱ��y��![]() x+
x+![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B����F�ǵ�B����x��ĶԳƵ㣬������y��
��x�ύ�ڵ�A����y�ύ�ڵ�B����F�ǵ�B����x��ĶԳƵ㣬������y��![]() x2+bx+c������A�͵�F����ֱ��AB���ڵ�C��
x2+bx+c������A�͵�F����ֱ��AB���ڵ�C��
��1����b��c��ֵ��
��2����P��ֱ��AC�·����������ϵ�һ���㣬����PA��PB�����PAB������������P��ֱ��AC�������룻
��3����Q����������һ�㣬��D���������ϣ��ڣ�2���������£��Ƿ������A��P��D��QΪ������APΪ�ߵ�ƽ���ı��Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ൺ�����������ߺͱ����������ٹ�·������ȫ��400ǧ�ף�����ȫ��320ǧ�ף��ס��������ͳ��ֱ������ߺͱ��ߴ��ൺʻ�����ϣ���֪�ͳ��������߸��ٹ�·����ʻ��ƽ���ٶȱȿͳ����ڱ��߸��ٹ�·�Ͽ�20ǧ��/Сʱ������ǡ��ͬʱ������ϣ��������ͳ����ൺ���������õ�ʱ���Ƕ���Сʱ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com