
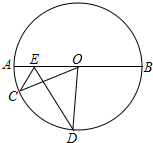
 如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD
如图,点E为⊙O的直径AB上一个动点,点C、D在下半圆AB上(不含A、B两点),且∠CED=∠OED=60°,连OC、OD分析 (1)延长CE交⊙O于D′,连接OD′,由已知求得∠AEC=60°,进而求得∠DEO=∠D′EO=60°,根据圆是轴对称图形即可证得∠D=∠D′,ED=ED′,然后根据等腰三角形的性质求得∠D′=∠C,从而证得结论;
(2)证得∠COD′>60°,从而证得CD′>OC=OD′,由CD′<OC+OD′,CE+ED=CE+ED′=CD′,从而得出r<CE+ED<2r.
解答 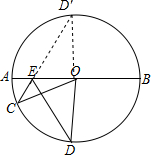 证明:(1)延长CE交⊙O于D′,连接OD′
证明:(1)延长CE交⊙O于D′,连接OD′
∵∠CED=∠OED=60°,
∴∠AEC=60°,
∴∠OED′=60°,
∴∠DEO=∠D′EO=60°,
由轴对称的性质可得∠D=∠D′,ED=ED′,
∵OC=OD′,
∴∠D′=∠C,
∴∠C=∠D;
(2)∵∠D′EO=60°,
∴∠C<60°,
∴∠C=∠D′<60°,
∴∠COD′>60°,
∴CD′>OC=OD′,
∵CD′<OC+OD′,
∵CE+ED=CE+ED′=CD′,
∴r<CE+ED<2r.
点评 本题考查了轴对称的性质,轴对称-最短路线问题,等腰三角形的性质,三角形外角的性质以及三角形三边之间的关系,圆是轴对称图形是本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知数轴上有三点A、B、C.
已知数轴上有三点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
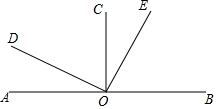 如图,己知直线AB上一点O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.
如图,己知直线AB上一点O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com