
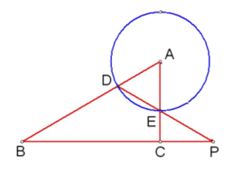
【题目】如图,在![]() 中,
中,![]() .半径为
.半径为![]() 的圆
的圆![]() 与边
与边![]() 相交于点
相交于点![]() 与边
与边![]() 相交于点
相交于点![]() 连结
连结![]() 并延长,与线段
并延长,与线段![]() 的延长线交于点
的延长线交于点![]() .
.
(1)当![]() 时,连结
时,连结![]() 若
若![]() 与
与![]() 相似,求
相似,求![]() 的长;
的长;
(2)若![]() 求
求![]() 的正切值;
的正切值;
(3)若![]() ,设
,设![]() 的周长为
的周长为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,其中
,其中![]()
【解析】
(1)当∠B=30°时,∠A=60°,此时△ADE是等边三角形,则∠PEC=∠AED=60°,由此可证得∠P=∠B=30°;若△AEP与△BDP相似,那么∠EAP=∠EPA=∠B=∠P=30°,此时EP=EA=1,即可在Rt△PEC中求得CE的长;
(2)若BD=BC,可在Rt△ABC中,由勾股定理求得BD、BC的长;过C作CF∥DP交AB于F,易证得△ADE∽△AFC,根据得到的比例线段可求出DF的长;进而可通过证△BCF∽△BPD,根据相似三角形的对应边成比例求得BP、BC的比例关系,进而求出BP、CP的长;在Rt△CEP中,根据求得的CP的长及已知的CE的长即可得到∠BPD的正切值;
(3)过点D作DQ⊥AC于Q,可用未知数表示出QE的长,根据∠BPD(即∠EDQ)的正切值即可求出DQ的长;在Rt△ADQ中,可用QE表示出AQ的长,由勾股定理即可求得EQ、DQ、AQ的长;易证得△ADQ∽△ABC,根据得到的比例线段可求出BD、BC的表达式,进而可根据三角形周长的计算方法得到y、x的函数关系式.
![]() 解:
解:![]()
![]()
![]()
![]()
![]()
![]() 三角形
三角形![]() 为等腰三角形
为等腰三角形
![]() 与
与![]() 相似
相似
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,
,
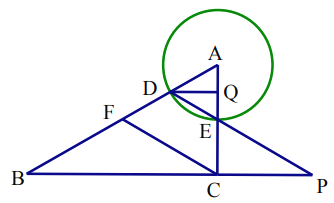
且设![]()
![]()
![]()
![]()
![]() 与
与![]() 相似
相似
![]()
即![]()
![]()
在![]() 中,
中,
![]()
![]()
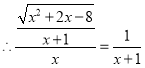
解之得![]() ,
,
即![]()
过点![]() 作
作![]()
![]() 与
与![]() 相似,
相似,
![]() ,
,
即![]() ,
,
即![]()
![]()
![]() 与
与![]() 相似
相似
![]() ,
,
即:![]()
![]()
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,
,
则![]() 与
与![]() 相似,
相似,
设![]() ,则
,则![]()
![]() 且
且![]()
![]()
![]() 在
在![]() 中,
中,
据勾股定理得:![]()
即:![]() ,
,
解之得![]() (舍去)
(舍去)![]()
![]() 与
与![]() 相似
相似
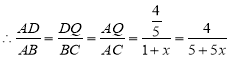
![]()
![]() 三角形
三角形![]() 的周长
的周长![]()
即:![]() ,其中
,其中![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程y(米)与时间x(分)的函数关系如图2所示.
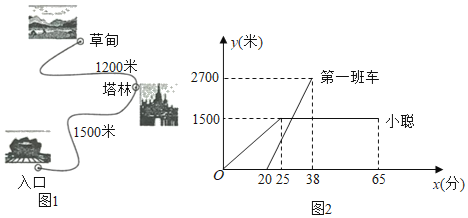
(1)求第一班车离入口处的路程y(米)与时间x(分)函数表达式.并写出x的取值范围;
(2)求第一班车从入口处到达塔林所需的时间;
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某场测试中各射击10次,两人的测试成绩如下:
甲 7 7 8 8 8 9 9 9 10 10
乙 7 7 7 8 8 9 9 10 10 10
这两人10次射击命中的环数的平均数![]() =
=![]() =8.5,则测试成绩比较稳定的是 .(填“甲”或“乙”)
=8.5,则测试成绩比较稳定的是 .(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:

(2)若把24分以上(含24分)记为”优秀”,两班各50名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中数据分布情况,请通过计算方差说明哪个班的学生纠错的得分情况更稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:![]() .)
.)
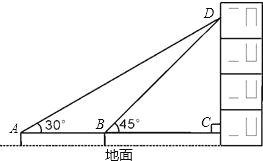
查看答案和解析>>
科目:初中数学 来源: 题型:
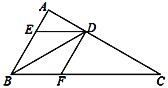
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
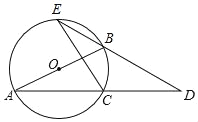
【题目】如图,AB是⊙O的直径,D是弦AC的延长线上一点,且CD=AC,DB的延长线交⊙O于点E.
(1)求证:CD=CE;
(2)连结AE,若∠D=25°,求∠BAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
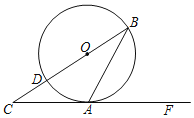
【题目】如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线CF交BD延长线于点C.
(Ⅰ)若∠C=25°,求∠BAF的度数;
(Ⅱ)若AB=AC,CD=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
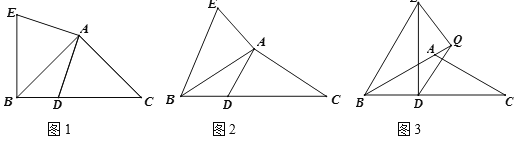
【题目】△ABC中,∠BAC=α°,AB=AC,D是BC上一点,将AD绕点A顺时针旋转α°,得到线段AE,连接BE.
(1)(特例感知)如图1,若α=90,则BD+BE与AB的数量关系是 .
(2)(类比探究)如图2,若α=120,试探究BD+BE与AB的数量关系,并证明.
(3)(拓展延伸)如图3,若α=120,AB=AC=4,BD=![]() ,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
,Q为BA延长线上的一点,将QD绕点Q顺时针旋转120°,得到线段QE,DE⊥BC,求AQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com